
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Sampling › Distribusi Sampling - Distribusi Fisher
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Distribusi Sampling - Distribusi Fisher
Dalam teori probabilitas dan statistika, distribusi F sering kali digunakan dalam pengujian statistika seperti analisis varians dan analisis regresi.
Distribusi F juga dikenal dengan sebutan distribusi F Snedecor atau distribusi Fisher Snedecor (merujuk pada R.A Fisher dan George W. Snedecor). Dalam teori probabilitas dan statistika, distribusi F sering kali digunakan dalam pengujian statistika seperti analisis varians dan analisis regresi.
Definisi dari distribusi F berikut ini.
Definisi:
Jika \(X_1 \sim χ^2 (n_1)\) dan \(X_2 \sim χ^2(n_2)\) adalah independen, maka variabel acak

mempunyai pdf berikut untuk \(y > 0:\)

Distribusi ini disebut disebut \(F\) dengan \(n_1\) dan \(n_2\) derajat bebas, dan dinotasikan dengan \(Y \sim F(n_1,n_2)\). Beberapa penulis menggunakan notasi \(F\) daripada \(Y\) untuk rasio ini.
Bukti:
Pembuktian yang akan diberikan berikut cukup rumit dan melibatkan teknik transformasi yang telah kita pelajari. Jika Anda kurang paham, bertanyalah kepada yang lain. Tidak perlu terlalu memaksakan diri.
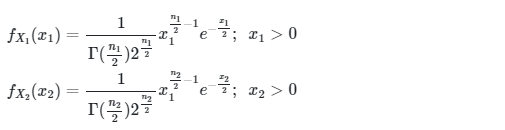

Misalkan,

Sehingga
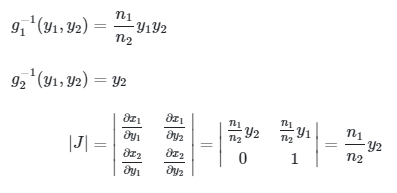
Dengan demikian, kita peroleh
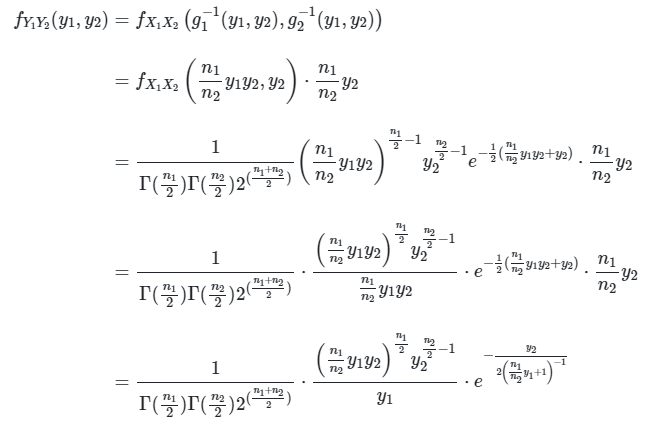
Fungsi kepekatan peluang (pdf) marginal \( Y_1 \) adalah

Selanjutnya, gunakan rumus berikut:

di mana:

Sehingga,
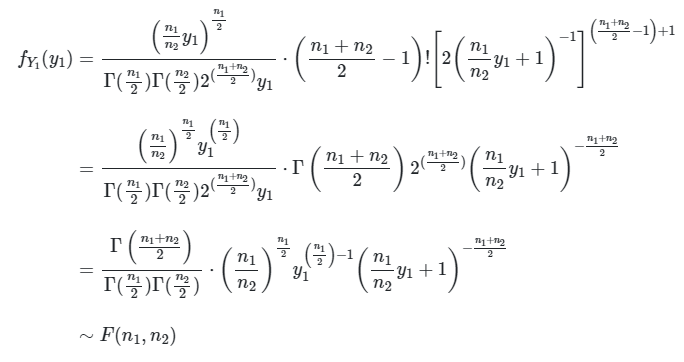
Teorema:
Jika \(X \sim F(v_1,v_2)\), maka
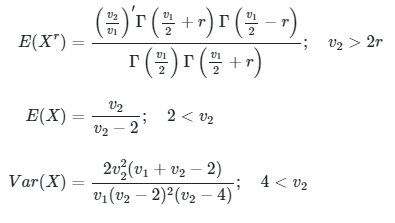
Teorema:
Misalkan \(X_1,X_2,…,X_{n_1}\) dan \(Y_1,Y_2,…,Y_{n_2}\) adaalah sampel acak dari populasi dengan distribusi \(X_i \sim N(μ_1,σ_1^2)\) dan \(Y_i \sim N(μ_2,σ_2^2)\). Jika \(v_1=n_1-1\) dan \(v_2=n_2-1\), maka \(\frac{v_1 S_1^2}{σ_1^2} \sim χ^2 (v_1)\) dan \(\frac{v_2 S_2^2}{σ_2^2} \sim χ^2 (v_2)\), sehingga

dan karena itu

dan
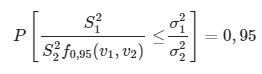
Artikel Terkait
Life without love is like a tree without blossoms or fruit.
Khalil Gibran