
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Bersama Peubah Acak › Distribusi Bersama Diskrit
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Joint Distribution
Distribusi Bersama Diskrit
Definisi:
Joint pdf dari k-dimensi random variabel diskrit \(X=(X_1,X_2,…,X_k)\) didefinisikan sebagai:

untuk seluruh kemungkinan nilai \(x = (x_1,x_2, …,x_k)\) dari X.
Definisi:
Joint CDF dari k-dimensi random variabel diskrit \(X_1, X_2,…,X_k\) adalah fungsi:
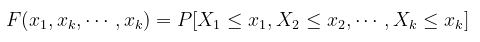
Teorema:
Fungsi \(f(x_1,…,x_k)\) merupakan joint pdf dari vektor \(X=(X_1,X_2,...,X_k)\) jika dan hanya jika berlaku:
- \(f(x_1,…,x_k )≥0\) untuk semua \(x_1,…,x_k\).
- \(∑_\limits{x_1} \dots ∑_\limits{x_k} f(x_1,x_2,..,x_k)=1 \)
Contoh 1: Diskrit joint probability distribusi hipergeometrik
Pada ruang pamer sebuah toko bunga terdapat 1000 batang bunga yang terdiri dari 400 batang warna merah, 400 batang warna putih dan 200 sisanya berwarna pink. Jika seorang pelanggan datang dan memilih 10 batang bunga, berapa probabilitas bahwa pelanggan tersebut akan memilih bunga merah sebanyak 2 batang, bunga putih sebanyak 5 batang dan sisanya adalah bunga pink?
Pembahasan:
Misal \(X_1\) = Banyaknya bunga merah yang terambil, \(X_2\) = Banyaknya bunga putih yang terambil, maka banyaknya bunga pink yang terambil adalah \((10-X_1-X_2)\), sehingga cukup didefinisikan dua peubah acak \(X_1\) dan \(X_2\) dengan joint probability:

Contoh 2: Diskrit joint probability for Extended hypergeometric distribution
Misal terdapat \(N\) buah obyek terdiri atas \(k+1\) tipe obyek yang berbeda dengan komposisi: Tipe 1 sebanyak \(M_1\), Tipe 2 sebanyak \(M_2\), seterusnya hingga Tipe ke \(k+1\) sebanyak \(M_{k+1}\). Kemudian diambil sampel sebanyak \(n\) buah tanpa pengembalian (Without replacement). Jika \(X_i\) menyatakan banyaknya item \(i\) yang diambil, maka vektor random \(X=(X_1,X_2,...,X_k)\) memiliki distribusi yang disebut extended hypergeometric distribution dengan pdf:

di mana:

Artikel Terkait
Kemuliaan manusia terletak pada pikirannya.
Pascal