Distribusi Bersyarat (Conditional Distribution)

Statistika Matematika I » Distribusi Bersama Peubah Acak › Distribusi Bersyarat (Conditional Distribution) - Rumus dan Contoh Soal

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Peubah Acak

Distribusi Bersyarat (Conditional Distribution) - Rumus dan Contoh Soal

Dalam teori peluang dan statistika, kita mengenal istilah distribusi bersyarat (conditional distribution). Pada tulisan ini, kita akan membahas cara mencari distribusi bersyarat dari suatu peubah acak disertai contoh soal dan pembahasannya.

Definisi: Distribusi Bersyarat

Jika \(X\) dan \(Y\) adalah peubah-peubah acak, baik diskrit maupun kontinu, dengan distribusi peluang bersama (joint pdf) adalah \(f(x,y)\), maka distribusi bersyarat (conditional distribution) dari \(Y\) dengan syarat \(X=x\) didefinisikan sebagai

Demikian pula, distribusi bersyarat untuk \(X\) dengan syarat \(Y=y\) adalah:

Contoh 1: Kasus Diskrit

Diketahui fungsi distribusi peluang bersama (joint pdf) dari peubah acak \(X\) dan \(Y\) adalah:

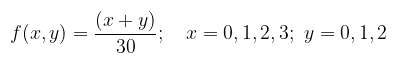
Carilah fungsi distribusi peluang bersyarat \(f(y│x=1)\).

Pembahasan:

Perhatikan bahwa ketika \(x=1\), maka joint pdf menjadi

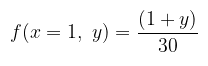
Untuk mencari \(f(y│x=1)\), pertama kita harus menemukan distribusi marginal dari \(X\). Dari artikel sebelumnya, kita peroleh

Ketika \(x=1\), maka distribusi marginal \(X\) menjadi

Dengan demikian, kita peroleh

Contoh 2: Kasus Kontinu

Jika diketahui pdf bersama (joint pdf) dari \(X\) dan \(Y\) adalah

Carilah pdf bersyarat dari \(Y\) jika diberikan \(X=x\) atau \(f(y|x)\) dan hitunglah \(P(Y>0│X=0,75)\).

Pembahasan:

Untuk mencari \(f(y│x)\), pertama kita harus menemukan distribusi marginal dari \(X\). Dari artikel sebelumnya, kita peroleh

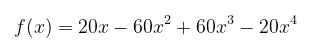
Dengan demikian, kita peroleh

Contoh 3: Kasus Diskrit

Jika \(X\) dan \(Y\) adalah dua buah variabel acak diskrit dan \( f(x,y) \) merupakan fungsi probabilitas bersama berbentuk

\begin{aligned} f(x,y) &= \frac{1}{21}(x+y); \quad x=1,2,3; y = 1,2 \end{aligned}

Tentukanlah \( f(x|y) \) dan \( f(y|x) \).

Pembahasan:

Pertama, kita perlu mencari distribusi marginal dari \(X\) dan \(Y\) terlebih dahulu. Sesuai definisi distribusi marginal, kita peroleh berikut:

\begin{aligned} f(x) &= \sum_{x} f(x,y) = \sum_{x=1}^3 \frac{1}{21}(x+y) \\[8pt] &= \frac{1}{21}(1+y) + \frac{1}{21}(2+y)+\frac{1}{21}(3+y) \\[8pt] &= \frac{(1+y)+(2+y)+(3+y)}{21} \\[8pt] &= \frac{6+3y}{21}; \quad y = 1,2 \\[8pt] f(y) &= \sum_y f(x,y) = \sum_{y=1}^2 \frac{1}{21}(x+y) \\[8pt] &= \frac{1}{21}(x+1)+\frac{1}{21}(x+2) \\[8pt] &= \frac{1}{21}(2x+3); \quad x=1,2,3 \end{aligned}

Dengan demikian, berdasarkan rumus distribusi bersyarat, kita peroleh berikut ini:

\begin{aligned} f(x|y) &= \frac{f(x,y)}{f(y)} = \frac{\frac{1}{21}(x+y)}{\frac{1}{21}(6+3y)} \\[8pt] &= \frac{x+y}{6+3y}; \quad x = 1,2,3 \\[8pt] f(y|x) &= \frac{f(x,y)}{f(x)} = \frac{\frac{1}{21}(x+y)}{\frac{1}{21}(2x+3)} \\[8pt] &= \frac{x+y}{2x+3}; \quad y=1,2 \end{aligned}

Contoh 4: Kasus Kontinu

Jika diketahui joint pdf antara \(X\) dan \(Y\) adalah

\begin{aligned} f(x,y) = \begin{cases} 10xy^2, &\quad 0 < x < y < 1 \\[1em] 0, &\quad x,y \ \text{lainnya} \end{cases} \end{aligned}

Carilah pdf marginal dari \(X\) dan pdf bersyarat \( f(y|x) \) serta hitunglah \( P(0,25 < Y < 0,5 | x = 0,25) \).

Pembahasan:

Pertama, kita cari dulu pdf marginal dari \(X\), yaitu:

\begin{aligned} f(x) &= \int_y f(x,y) \ dy = \int_x^1 10xy^2 \ dy \\[8pt] &= \left[ \frac{10}{3}xy^3 \right]_x^1 = \frac{10}{3}x-\frac{10}{3}x^4 \\[8pt] &= \frac{10}{3}x(1-x^3); \quad 0 < x < 1 \end{aligned}

Dengan demikian, kita peroleh berikut:

\begin{aligned} f(y|x) &= \frac{f(x,y)}{f(x)} = \frac{10xy^2}{\frac{10}{3}x(1-x^3)} \\[8pt] &= \frac{3y^2}{1-x^3}; \quad 0 < y < 1 \\[8pt] P(0,25 < Y < 0,5|x=0,25) &= \int_y f(y|x=0,25) \ dy \\[8pt] &= \int_{0,25}^{0,5} \frac{3y^2}{1-(0,25)^2} \ dy \\[8pt] &= \frac{3}{1-(0,25)^2} \int_{0,25}^{0,5} y^2 \ dy \\[8pt] &= \frac{64}{21} \left[ \frac{1}{3}y^3 \right]_{0,25}^{0,5} = \frac{64}{21} \left[ \frac{1}{3}(0,5)^3-\frac{1}{3}(0,25)^3 \right] \\[8pt] &= \frac{64}{21} \times \frac{1}{3} \left[ 0,5^3-0,25^3 \right] \\[8pt] &= \frac{64}{63} \times \frac{7}{64} = \frac{1}{9} \end{aligned}

Contoh 5: Kasus Kontinu

Diketahui joint pdf antara \(X\) dan \(Y\) adalah sebagai berikut:

\begin{aligned} f(x,y) = \begin{cases} 8xy, &\quad 0 < x < y < 1 \\[1em] 0, &\quad x,y \ \text{lainnya} \end{cases} \end{aligned}

Tentukan \( f(y|x), \ f(x|y), \) dan \( P(x \leq 0,5 | y = 0,75) \).

Pembahasan:

Pertama, kita cari distribusi marginal untuk \(X\) dan \(Y\) terlebih dahulu.

\begin{aligned} f(x) &= \int_y f(x,y) \ dy = \int_x^1 8xy \ dy \\[8pt] &= \left[ 4xy^2 \right]_x^1 = 4x-4x^3 \\[8pt] &= 4x(1-x^2); \quad 0 < x < 1 \\[8pt] f(y) &= \int_x f(x,y) \ dx = \int_0^y 8xy \ dx \\[8pt] &= \left[ 4x^2y \right]_0^y = 4y^3; \quad 0 < y < 1 \end{aligned}

Dengan demikian, kita peroleh berikut ini:

\begin{aligned} f(y|x) &= \frac{f(x,y)}{f(x)} = \frac{8xy}{4x(1-x^2)} \\[8pt] &= \frac{2y}{1-x^2}; \quad 0 < x < y < 1 \\[8pt] f(x|y) &= \frac{f(x,y)}{f(y)} = \frac{8xy}{4y^3} \\[8pt] &= \frac{2x}{y^2}; \quad 0 < x < y < 1 \\[8pt] P(x \leq 0,5 | y = 0,75) &= \int_x f(x|y=0,75) \ dx \\[8pt] &= \int_0^{0,5} \frac{2x}{y^2} \ dx = \int_0^{0,5} \frac{2x}{(0,75)^2} \ dx \\[8pt] &= \frac{2}{(0,75)^2} \int_0^{0,5} x \ dx = \frac{32}{9} \left[ \frac{1}{2}x^2 \right]_0^{0,5} \\[8pt] &= \frac{32}{9} \cdot \frac{1}{2}(0,5)^2 = \frac{4}{9} \end{aligned}

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

STATISTIKA MATEMATIKA I

Statistika Matematika I » Distribusi Bersama Peubah Acak › Distribusi Bersyarat (Conditional Distribution) - Rumus dan Contoh Soal

Peubah Acak