Nilai Harapan Bersyarat (Conditional Expected Value)

Statistika Matematika I » Sifat Peubah Acak › Nilai Harapan Bersyarat (Conditional Expected Value) - Rumus dan Contoh Soal

Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552

Peubah Acak

Nilai Harapan Bersyarat (Conditional Expected Value) - Rumus dan Contoh Soal

Dalam tulisan ini, kita akan membahas tentang cara mencari nilai harapan bersyarat (conditional expected value) dari suatu peubah acak.

Pada tulisan sebelumnya, kita telah membahas tentang distribusi bersyarat (conditional distribution). Dalam kesempatan ini, kita akan lanjutkan ke materi yang masih berkaitan dengan distribusi bersyarat yaitu mencari nilai harapan bersyarat (conditional expected value) dari suatu peubah acak.

Kita berikan definisi mengenai nilai harapan bersyarat berikut ini:

Definisi:

Misalkan \(X\) dan \(Y\) adalah peubah acak bersama (joint random variable), maka nilai harapan \(Y\) dengan syarat \(X=x\) adalah:

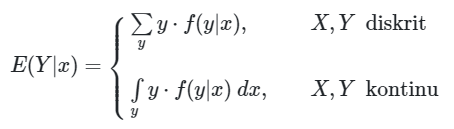
Contoh notasi penulisan yang lain:

Contoh 1:

Jika diketahui:

Nilai harapan bersyaratnya adalah:

\(E_Y(Y│x)\) merupakan fungsi dari \(x\). Jadi, \(E_Y (Y│x)\) dapat dipandang sebagai obyek baru (random variable) yang bergantung pada nilai \(x\).

Teorema:

Jika \(X\) dan \(Y\) adalah distribusi bersama random variables, maka

Bukti: (kasus kontinu)

Contoh 2:

Diketahui \(X\) adalah variabel random yang berdistribusi Bernoulli dengan parameter "\(p\)" atau \(X \sim Ber(p)\). Misalkan \(E(Y│X=0)=1\) dan \(E(Y│X=1)=2\). Jika \(p = ½\), berapa nilai \(E(Y)\)?

Pembahasan:

Diketahui:

Jika \(p=1/2\), maka

Teorema:

Jika \(X\) dan \(Y\) adalah random variables independen, maka \(E(Y│x)=E(Y)\) dan \(E(X│y)=E(X)\).

Bukti:

Jika \(X\) dan \(Y\) adalah independen, maka \(f(x,y)=f(x)⋅f(y)\) sehingga \(f(y│x)=f(y)\) dan \(f(x│y)=f(x)\). Dalam kasus kontinu,

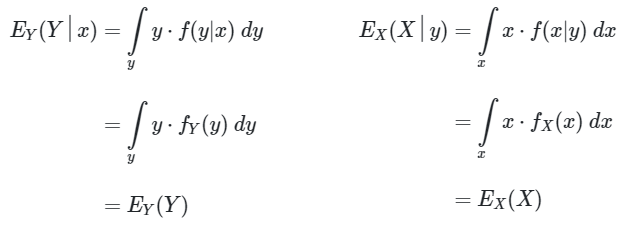
Untuk kasus diskrit bisa dicari dengan cara serupa.

Varians Bersyarat (Conditional Variance)

Selain nilai harapan bersyarat di atas, konsep penting terkait peubah acak yang akan kita pelajari yaitu varians bersyarat (conditional variance). Kita dapat menggunakan rumus nilai harapan bersyarat di atas untuk mencari varians bersyarat dari suatu peubah acak. Kita berikan definisi dan beberapa teorema terkait varians bersyarat berikut ini.

Definisi:

Varians bersyarat dari \(Y\) dengan syarat \(X=x\) diberikan oleh

\[ Var(Y|x) = E(Y^2|x) - \left[ E(Y|x) \right]^2 \]

Teorema:

Jika \(X\) dan \(Y\) adalah distribusi bersama peubah acak, maka

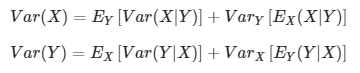
Bukti: (i)

Bukti: (ii)

Teorema:

Jika \(X\) dan \(Y\) adalah distribusi bersama peubah acak dan \(h(x,y)\) merupakan sebuah fungsi, maka

\[ E[h(x,y)] = E_X [E(h(x,y)|X)] \]

Teorema:

Jika \(X\) dan \(Y\) adalah distribusi bersama peubah acak dan \(g(x)\) merupakan sebuah fungsi, maka

\[ E \left[ g(x) Y|x \right] = g(x)E(Y|x) \]

Teorema:

Jika \(E(Y│x)\) merupakan fungsi linear dari \(x\), maka

\[ E(Y|x) = μ_2 + \rho \frac{σ_2}{σ_1} (x-μ_1) \]

dan

\[ E_x \left[ Var(Y|X) \right] = σ_2^2 (1-\rho^2) \]

Bukti:

Jika \(E(Y│x)=ax+b\), maka

dan

Sehingga,

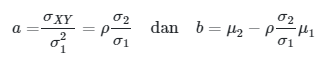
Berikutnya,

Perhatikan bahwa jika varians bersyarat tidak bergantung pada \(x\), maka

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

STATISTIKA MATEMATIKA I

Statistika Matematika I » Sifat Peubah Acak › Nilai Harapan Bersyarat (Conditional Expected Value) - Rumus dan Contoh Soal

Peubah Acak