Statistika Matematika I   »   Distribusi Sampling   ›  Distribusi Sampling - Distribusi Normal

Peubah Acak

Distribusi Sampling - Distribusi Normal

Distribusi peluang peubah acak normal bergantung pada dua parameter \(μ\) dan \(σ\), yaitu rataan dan simpangan bakunya.

Suatu peubah acak X yang distribusinya berbentuk lonceng seperti pada Gambar 1 di bawah disebut peubah acak normal. Distribusi peluang peubah acak normal bergantung pada dua parameter \(μ\) dan \(σ\), yaitu rataan dan simpangan bakunya.

Jadi, fungsi kepadatan peluang X yang berdistribusi normal dinyatakan sebagai berikut:

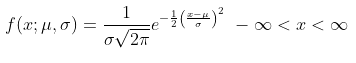
Dalam beberapa literatur, distribusi normal biasa disingkat juga dengan notasi \(n(x;μ,σ)\).

Gambar 1. Kurva normal

Teorema:

Jika \(X_i \sim N(μ_i,σ_i^2); \ i=1,…,n\) menunjukkan variabel independen yang berdistribusi normal, maka

Teorema:

Jika \(X_1,X_2,…,X_n\) menunjukkan sampel acak dari \(N(μ,σ^2)\), maka

Teorema:

Jika \(X_1,X_2,…,X_n\) menunjukkan sampel acak dari \(N(μ,σ^2)\), maka

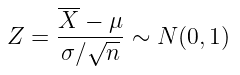
Bukti:

Untuk pembuktian teorema ini, kita bisa menerapkan sifat MGF berikut:

Dengan sedikit manipulasi, kita peroleh

sehingga \(a= \frac{-μ}{σ/\sqrt{n}}\) dan \(b= \frac{1}{σ/\sqrt{n}}\). Dengan demikian, kita peroleh

Perhatikan bahwa \( e^{\frac{1}{2}t^2} \) merupakan mgf normal standard. Dengan demikian, \(Z= \frac{\overline{X}-μ}{σ/\sqrt{n}}\) akan mengikuti distribusi normal dengan rata-rata 0 dan varians 1.

Catatan:

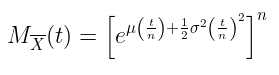
Teorema:

Misalkan dua sampel acak independen \(X_1,X_2,…,X_{n_1}\) dan \(Y_1,Y_2,…,Y_{n_2}\), dengan masing-masing sampel \(n_1\) dan \(n_2\), dari populasi berdistribusi normal, \(X_i \sim N(μ_1,σ_1^2)\) dan \(Y_j \sim N(μ_2,σ_2^2)\) dan notasikan \(\overline{X}\) dan \(\overline{Y}\) sebagai rata-rata sampel acak. Maka perbedaan rata-rata kedua sampel acak akan berdistribusi normal yakni

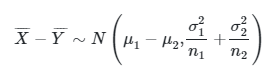
Bukti:

Kita tahu bahwa MGF distribusi normal yaitu

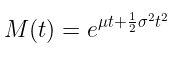
Dengan demikian,