
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Peubah Acak › Distribusi Peubah Acak Kontinu
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Distribusi Peubah Acak
Distribusi Peubah Acak Kontinu
Banyak kejadian atau peristiwa dalam kehidupan kita sehari-hari yang mengikuti distribusi peubah acak kontinu.
Bila ruang sampel mengandung titik sampel yang takberhingga banyaknya dan banyaknya sebanyak titik pada sepotong garis, maka ruang sampel itu disebut ruang sampel kontinu dan peubah acak yang didefinisikan tersebut disebut peubah acak kontinu.
Banyak kejadian atau peristiwa dalam kehidupan sehari-hari yang mengikuti salah satu dari distribusi peubah acak kontinu yang akan diberikan berikut ini.
Distribusi Uniform Kontinu
Suatu peubah acak X pada interval (a,b) dikatakan berdistribusi uniform kontinu jika nilai f(x) adalah tetap untuk tiap x dalam interval (a,b) dengan fungsi pdf
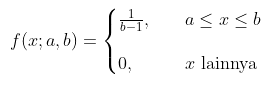
Rataan dan Varians
Rata-rata dan variansi distribusi uniform adalah

Moment Generating Function
Andaikan X adalah variabel acak kontinu yang mengikuti distribusi uniform. MGF dari X diberikan oleh:

Distribusi Normal
Fungsi padat peubah acak normal X, dengan rataa μ dan variansi σ2, ialah

di mana π=3,14159… dan e=2,71828…
Rataan dan Varians
Rataan suatu peubah acak yang berdistribusi normal adalah μ, sedangkan variansnya σ2.
Moment Generating Function
MGF distribusi normal diberikan oleh
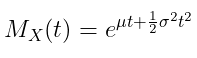
Distribusi Gamma
Peubah acak kontinu X berdistribusi gamma, dengan parameter α dan β, bila fungsi padatnya berbentuk

di mana α>0 dan β>0.
Rataan dan Varians
Rataan dan variansi distribusi gamma adalah μ=αβ dan σ2=αβ2.
Moment Generating Function
MGF disribusi gamma diberikan oleh
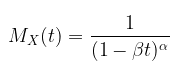
Distribusi Eksponensial
Peubah acak kontinu X akan berdistribusi eksponensial, dengan parameter θ, bila fungsi padatnya berbentuk
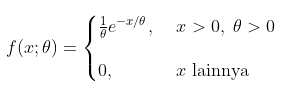
Rataan dan Varians
Rataan dan varians distribusi eksponensial adalah μ=θ dan σ2=θ2
Moment Generating Function
Andaikan X adalah variabel acak kontinu yang mengikuti distribusi eksponensial. MGF dari X diberikan oleh:

Distribusi Chi-Square
Peubah acak kontinu X berdistribusi Khi-Kuadrat, dengan derajat bebas v, bila fungsi padatnya diberikan oleh

dengan v bilangan bulat positif.
Rataan dan Varians
Nilai harapan atau rataan distribusi khi-kuadrat diberikan oleh μ=v dan variansinya adalah σ2=2v
Moment Generating Function
MGF Distribusi Chi-Square diberikan oleh
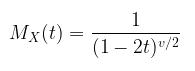
Distribusi Student-t
Kita bisa mendefinisikan peubah acak T yang mengikuti distribusi student-t sebagai rasio dari peubah acak normal baku Z terhadap peubah acak khi-kuadrat V dengan derajat bebas v.
Definisi:
Misalkan Z peubah acak normal baku dan V peubah acak khi-kuadrat dengan derajat bebas v. Bila Z dan V adalah peubah acak yang independen, maka distribusi dari

diberikan oleh

Ini dikenal dengan nama distribusi-t dengan derajat bebas v.
Rataan dan Varians
Rataan dan varians distribusi student-t diberikan oleh
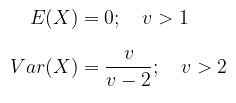
Distribusi Fisher
Dalam teori probabilitas dan statistika, distribusi F sering kali digunakan dalam pengujian statistika seperti analisis varians dan analisis regresi.
Suatu peubah acak yang mengikuti distribusi F bisa didefinisikan sebagai rasio dua peubah acak khi-kuadrat yang independen, masing-masing dibagi dengan derajat kebebasannya. Jadi, dapat ditulis

di mana U dan V menyatakan peubah acak bebas, masing-masing berdistribusi khi-kuadrat dengan derajat bebas v1 dan v2.
Definisi:
Misalkan U dan V dua peubah acak bebas masing-masing berdistribusi khi-kuadrat dengan derajat bebas v1 dan v2, maka distribusi peubah acak

diberikan oleh

Ini dikenal dengan nama distribusi-F dengan derajat bebas v1 dan v2.
Derajat bebas dari peubah acak khi-kuadrat pada pembilang F selalu ditulis lebih dahulu, kemudian diikuti oleh derajat bebas dari peubah acak khi-kuadrat yang muncul pada penyebut. Jadi kurva distribusi F tidak hanya tergantung pada kedua parameter v1 dan v2 tapi juga pada urutan keduanya ditulis.
Rataan dan Varians
Rataan dan varians distribusi Fisher diberikan oleh
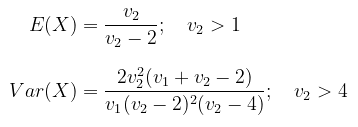
Distribusi Beta
Suatu peubah acak kontinu X dikatakan berdistribusi beta dengan parameter α>0 dan β>0 jika fungsi kepadatan peluangnya diberikan oleh
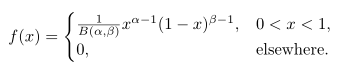
Rataan dan varians
Rata-rata dan varians distribusi beta dengan parameter α dan β

Artikel Terkait
The greatest danger for most of us is not that our aim is too high and we miss it, but that it is too low and we reach it.
Michelangelo