
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Fungsi Peubah Acak › Teknik CDF untuk Mencari Distribusi Peubah Acak Baru
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Teknik CDF untuk Mencari Distribusi Peubah Acak Baru
Teknik CDF digunakan untuk mencari distribusi suatu peubah acak baru dengan menurunkan CDF dari suatu peubah acak yang lain.
Kita mulai pembahasan dengan pertanyaan berikut: Bagaimana mencari distribusi dari suatu fungsi peubah acak baru berdasarkan fungsi dari peubah acak lain yang diketahui? Misalnya, jika \(Y\) menyatakan umur suatu komponen dalam satuan minggu dan \(X\) menyatakan umur suatu komponen dalam satuan hari, maka \(Y = 7X\). Anggaplah distribusi dari peubah acak X telah diketahui, lalu bagaimana distribusi dari peubah acak baru, \(Y\), ini?
Pada umumnya, terdapat tiga teknik yang bisa diterapkan untuk menemukan distribusi dari fungsi peubah acak baru ini, yakni
- Teknik fungsi distribusi kumulatif (CDF)
- Teknik transformasi
- Teknik fungsi pembangkit momen atau moment generating function (MGF)
Perlu diketahui bahwa walaupun untuk keadaaan tertentu ketiga teknik tersebut dapat digunakan, pada umumnya untuk suatu masalah tertentu, penggunaan salah satu cara akan lebih menguntungkan dari pada yang lain, dalam arti lebih mudah diterapkan.
Pada artikel ini kita akan secara khusus membahas teknik fungsi distribusi kumulatif (teknik CDF), sedangkan teknik lain akan dibahas pada artikel lain.
Teknik CDF
Sesuai dengan namanya, teknik ini berkenaan dengan distribusi kumulatif suatu fungsi. Intinya, teknik ini mencari distribusi peubah acak dengan menurunkan CDF dari suatu peubah acak yang lain. Kita nyatakan definisinya secara sebagai berikut.
Definisi:
Andaikan \(X\) adalah peubah acak yang mempunyai CDF \(F_X(x)\), dan misalkan \( Y \) adalah fungsi dari \( X \), yakni \(Y=g(x)\) yang juga memiliki bentuk CDF yang sama. Dengan demikian, kita bisa menyatakan CDF dari \(Y\) dalam bentuk yang sama dengan CDF dari \(X\).

Fungsi kepekatan peluang (pdf) dari \(y\) dapat dicari dengan menurunkan atau menderivasi fungsi CDF, yakni
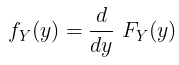
Contoh 1:
Misalkan peubah acak \(X\) menyatakan produksi suatu mesin giling padi menjadi beras per hari (dalam satuan ton). Dalam hal ini \(X\) merupakan peubah acak, karena produksi per hari akan bergantung pada operator, kondisi mesin, kondisi gabah yang digiling dan lain-lain. Misalnya pdf dari \(X\) adalah \[f(x)=2x,0≤x≤1\]
Jika untuk setiap ton beras mendapat bayaran 300 ribu dengan overhead cost sebesar 100 ribu, maka keuntungan per ton penggilingan padi adalah: \(Y=3X-1\) (dalam satuan ratus ribu)
Untuk keperluan estimasi peluang keuntungan, perlu diketahui pdf dari \(Y\). \(Y\) adalah sebuah peubah acak kontinu yang merupakan fungsi dari satu buah peubah acak lain yaitu \(X\) atau secara umum \(Y=g(X)=3X-1\).
Sekarang, mari kita cari cdf dari \(Y\) berdasarkan definisi yang telah kita berikan di atas.

Selanjutnya, cari batas nilai peubah acak \(X\) dan nilai peubah acak \(Y\).

Dengan demikian, CDF dari \(Y\) diberikan oleh
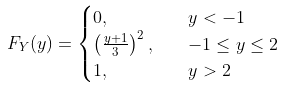
Sehingga PDF dari \(Y\) adalah
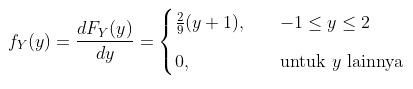
Contoh 2:
Andaikan \(X\) suatu peubah acak kontinu dengan fungsi CDF nya yaitu \(F_X(x)=1-e^{-2x}, \ 0 < x < \infty\), dan anggaplah \(Y=e^x\). Carilah distribusi (pdf) dari \( y \).
Pembahasan:
Dengan menerapkan teknik cdf, kita peroleh
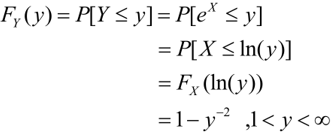
Untuk penentuan batasnya, perhatikan berikut.

Sehingga pdf dari \(Y\) adalah

Contoh 3:
Misalkan \(X\) adalah peubah acak kontinu, dan andaikan \(Y=X^2\). Tentukanlah distribusi dari peubah acak baru \(Y\) tersebut.
Pembahasan:
Dengan menerapkan teknik cdf, kita peroleh

Dengan demikian, pdf dari \(Y\) yaitu
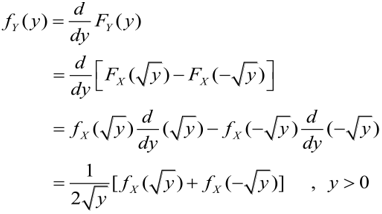
Sejauh ini contoh yang diberikan hanya dalam kasus satu peubah. Teknik CDF juga bisa diperluas untuk fungsi beberapa peubah, meskipun analisisnya akan menjadi lebih rumit. Kita nyatakan dalam teorema berikut:
Teorema:
Misalkan \(X=(X_1,X_2,…,X_k)\) adalah vektor \(k\)-dimensi dari peubah acak kontinu dengan joint pdf \(f(x_1,x_2,…,x_k)\). Jika \( Y \) adalah fungsi dari \(X\), yakni \(Y = u(X)\), maka
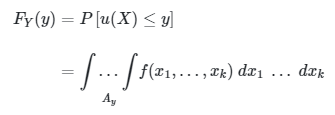
di mana \(A_y=\{x|u(x)≤y\}\)
Contoh 4:
Misalkan \(Y=X_1+X_2\), di mana \(X_i \sim EXP(1)\) dan \(x≥0\). Bagaimanakah distribusi dari \(f_Y (y)\) ?
Pembahasan:
Himpunan daerah yang memenuhi untuk kasus di atas adalah

Perhatikan gambar berikut:

Gambar: Daerah \(Ay\) sehingga \(x_1+x_2≤y\)
Dengan menggunakan teorema di atas, kita peroleh
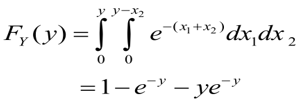
Sehingga pdf dari \(y\) adalah
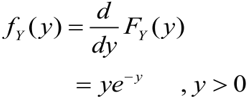
Artikel Terkait
Segala sesuatunya menjadi baik bagi orang yang berusaha sebaik-baiknya mengusahakan segala sesuatu.
John Wooden