
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA I
Statistika Matematika I
Peubah Acak dan Distribusi Peubah Acak
Distribusi Bersama Peubah Acak
Sifat Peubah Acak
Distribusi Fungsi Peubah Acak
Distribusi Sampling
Statistika Matematika I » Distribusi Fungsi Peubah Acak › Teknik Transformasi Satu-Satu
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Peubah Acak
Teknik Transformasi Satu-Satu
Teknik transformasi untuk mencari distribusi suatu peubah acak baru dapat dibagi jadi dua yakni transformasi satu-satu dan transformasi yang bukan satu-satu.
Pada umumnya terdapat tiga teknik untuk mencari distribusi dari suatu peubah acak yakni teknik CDF, teknik transformasi, dan teknik MGF. Kita telah membahas teknik CDF, dan sekarang kita akan lanjutkan dengan teknik transformasi.
Teknik transformasi ini dapat dibagi jadi dua yakni transformasi satu-satu dan transformasi yang bukan satu-satu. Pada artikel ini kita fokus pada teknik transformasi yang satu-satu, dan teknik transformasi yang bukan satu-satu disajikan pada artikel berikutnya.
Transformasi Satu-Satu Kasus Peubah Acak Diskrit \(X\)
Misalkan \(X\) adalah peubah acak diskrit dengan pdf \(f_X (x)\). Jika \(Y = g(X)\) merupakan transformasi satu-satu, maka fungsi pdf dari \(Y\) adalah

di mana \(B=\{y|f_Y (y)>0\}\) dan \(g^{-1}\) merupakan fungsi kebalikan umum.
Buki:
Karena \(Y = g(X)\) adalah fungsi satu-satu yang memetakan \(Y\) ke \(X\), maka untuk setiap nilai \(y=f(x)\) terdapat tepat satu nilai \(x = g^{-1} (y)\), sehingga:

di mana \(B=\{y|f_Y (y)>0\}\).
Contoh 1: Kasus Diskrit
Misalkan peubah acak \(X\) mengikuti distribusi geometri dengan parameter \(p\), yakni \(X \sim Geo(p)\) dan \(f_X (x) = pq^{x-1}; \ x=1,2,3,…\). Tentukan pdf dari \(Y = X-1\).
Pembahasan:
Karena \( y = x - 1 \), maka \( x = y + 1 = g^{-1}(y) \). Sehingga pdf dari \( Y \) adalah
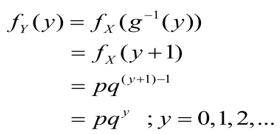
Transformasi Satu-Satu Kasus Peubah Acak Kontinu \(X\)
Misalkan \(X\) adalah peubah acak kontinu dengan pdf \(f_X (x)\). Jika \(Y = g(X)\) merupakan transformasi satu-satu dari \(A=\{x|f_X (x)>0\}\) ke \(B=\{y|f_Y (y)>0\}\), maka fungsi pdf dari \(Y\) adalah

dengan syarat turunan (derivative) \(\frac{d}{dy} (g^{-1} (y))\) adalah kontinu dan taknol dalam \(B\).
Bukti:
Pada kasus kontinu maka fungsi satu-satu hanya memiliki satu di antara 2 kemungkinan yaitu:
- Fungsi tersebut monoton naik (monotonic increasing): \(a>b⇒f(a)>f(b)\)
- Fungsi tersebut monoton turun (monotonic decreasing): \(a>b⇒f(a) < f(b)\)
Dalam teori peluang kita tahu bahwa \(F_X (x)\) adalah fungsi yang monoton naik dan \(1-F_X (x)\) adalah fungsi monoton turun. Perhatikan gambar berikut.

Gambar: Fungsi monoton naik dan fungsi monoton turun.
Karena sifat \(F_X (x)\) dan \(1-F_X (x)\) yang monoton tersebut maka aplikasi metode transformasi dilakukan melalui salah satu dari kedua fungsi tersebut, sebagai berikut:
Jika \(Y = g(X)\) merupakan fungsi naik (increasing function) maka \(g(x)≤y ↔x≤g^{-1} (y)\), sehingga kita gunakan \(F_X (x)\) untuk menurunkan fungsi \(f_Y (y)\) sebagai berikut:

Dengan demikian,
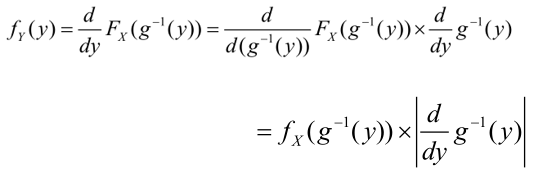
Jika \(Y = g(X)\) merupakan fungsi turun (decreasing function) maka \(g(x)≤y ↔x≥g^{-1} (y)\), sehingga kita gunakan \(1-F_X (x)\) untuk menurunkan fungsi \(f_Y (y)\) sebagai berikut:

Dengan demikian,

Contoh 2: Kasus Kontinu
Misalkan diketahui \( F_X(x) = 1 - e^{-2x}, \quad 0 < x < \infty \). Jika \( Y = e^X \), tentukanlah distribusi dari \(Y\).
Pembahasan:
Kita cari pdf dari \(X\) terlebih dahulu, yakni
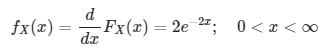
Karena \( y = e^x \), maka \( x = \ln y = g^{-1} (y) \). Sehingga

Dengan demikian, fungsi pdf dari \(Y\) yaitu

Contoh 3: Kasus Kontinu
Jika diketahui \( f_X(x) = 1; 0 < x < 1 \). Tentukan pdf dari \( Y = e^X \).
Pembahasan:
Karena \(y = e^x\), maka \( x = \ln y = g^{-1} (y) \). Sehingga

Dengan demikian, pdf dari \(Y\) adalah
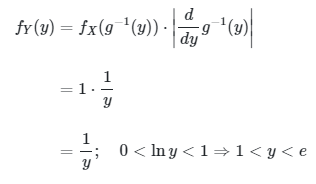
Contoh 4: Kasus Kontinu
Andaikan \(X\) mempunyai fungsi kepekatan peluang (pdf)
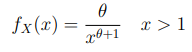
dan nol untuk \(x\) lainnya, di mana \(θ\) adalah parameter positif. Ini merupakan contoh distribusi Pareto. Tentukanlah pdf dari \(Y=\ln X\).
Pembahasan:
Karena \(x > 1\) maka \(y > 0\) dan invers transformasinya adalah \(x=e^y\) dan \(dx/dy=e^y\). Dengan demikian,

Perhatikan bahwa fungsi pdf dari \(Y\) adalah pdf untuk distribusi eksponensial.
Transformasi Bersama (Joint Transformations)
Teorema-teorema yang telah kita bahas sebelumnya dapat diperluas untuk fungsi beberapa peubah acak.
Definisi: Kasus Diskrit
Andaikan \(X_1, X_2\) mempunyai pdf bersama \(f_{X_1,X_2} (x_1,x_2)\). Misalkan \(Y_1=g_1 (X_1,X_2)\) dan \(Y_2=g_2 (X_1,X_2)\). Jika \(y_1=g_1 (x_1,x_2)\) dan \(y_2=g_2 (x_1,x_2)\) adalah transformasi satu-satu, maka \(x_1=g_1^{-1} (y_1,y_2)\) dan \(x_2=g_2^{-1} (y_1,y_2)\). Dengan demikian, joint pdf dari \(Y_1\) dan \(Y_2\) adalah

Definisi: Kasus Kontinu
Andaikan \(X_1, X_2\) mempunyai pdf bersama \(f_{X_1,X_2} (x_1,x_2)\). Misalkan \(Y_1=g_1 (X_1,X_2)\) dan \(Y_2=g_2 (X_1,X_2)\). Jika \(y_1=g_1 (x_1,x_2)\) dan \(y_2=g_2 (x_1,x_2)\) adalah transformasi satu-satu, maka \(x_1=g_1^{-1} (y_1,y_2)\) dan \(x_2=g_2^{-1} (y_1,y_2)\). Kemudian jika |J|, yang diberikan oleh

adalah determinan Jacobian transformasi. Maka joint pdf dari \(Y_1\) dan \(Y_2\) adalah
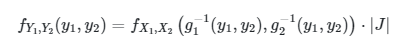
Contoh 5: Kasus Kontinu
Andaikan \(X_1\) dan \( X_2 \) mempunyai joint pdf

Dengan transformsi \( y_1 = x_1 \) dan \( y_2 = x_1 + x_2 \), kita peroleh \( x_1 = y_1 \) dan \( x_2 = y_2 - y_1 \). Himpunan \( B = \{ (y_1,y_2): 0 \leq y_1 \leq y_2 \leq \infty \} \). Nilai Jacobian adalah
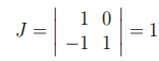
Dengan demikian, joint pdf dari \( Y_1 \) dan \( Y_2 \) diberikan oleh
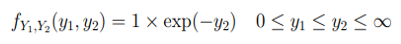
Jika kita hanya ingin mencari pdf dari \( Y_2 = X_1 + X_2 \), kita harus mencari pdf marginal dari \( Y_2 \) dengan mengintegralkan keluar \(Y_1\). Kita peroleh

Contoh 6: Kasus Kontinu
Jika diketahui \(X_1\) dan \( X_2 \) mempunyai joint pdf

Andaikan kita ingin mencari pdf dari \( Y_1 = X_1/X_2 \). Kita perlu peubah lain di sini, yakni \( Y_2 = X_2 \). Kita pilih peubah \( Y_2 \) agar kita bisa mencari invers dengan mudah. Inversnya adalah \( x_1 = y_1y_2 \) dan \( x_2 = y_2 \). Nilai Jacobian adalah
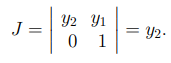
Kita punya \( A = \{ 0 < x_1 < x_2 < 1 \} \), maka \( B = \{ 0 < y_1y_2 < y_2 < 1 \} \) atau \( B = \{ 0 < y_1 < 1, 0 < y_2 < 1 \} \). Sehingga,
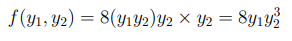
Dengan demikian, pdf marginal dari \( Y_1 \) adalah

Artikel Terkait
Jika seorang pemimpin tahu bagaimana memasuki suatu urusan, maka ia harus tahu juga bagaimana cara keluar dari urusan itu, sesempit apapun jalan keluar yang tersedia.
Amir bin Ash