Metode Statistika II   »   Uji Normalitas   ›  Uji Normalitas dengan Goodness of Fit Test

Normalitas

Uji Normalitas dengan Goodness of Fit Test

Goodness of Fit Test digunakan untuk menentukan apakah suatu data berasal dari suatu populasi dengan distribusi teoritis tertentu (misalnya normal, seragam, atau poisson).

---

Sampai sejauh ini, kita telah membicarakan pengujian hipotesis mengenai satu parameter populasi, seperti \(μ,σ^2\) dan \(p\). Sekarang kita akan membahas suatu uji untuk menentukan apakah suatu populasi memiliki sebaran teoretis tertentu (normal, seragam, atau poisson).

Uji ini didasarkan pada seberapa baik kesesuaian antara frekuensi yang teramati dalam data sampel dengan frekuensi harapan yang didasarkan pada sebaran yang dihipotesiskan.

Sebagai gambaran, perhatikan percobaan pelemparan sebuah dadu. Kita hipotesiskan bahwa dadu itu setimbang, yang mana ekivalen dengan pengujian hipotesis bahwa sebaran hasil percobaan itu adalah seragam.

\[ f(x) = \frac{1}{6}, \ x = 1, 2, ...,6 \]

Misalkan bahwa dadu tersebut dilemparkan 120 kali dan setiap hasilnya dicatat. Secara teoritis, bila dadu itu setimbang, kita mengharapkan bahwa setiap sisi muncul 20 kali. Hasil percobaan ini dicantumkan dalam Tabel 1.

Tabel 1. Frekuensi teramati dan harapan bagi 120 lemparan sebuah dadu

Dengan membandingkan frekuensi yang teramati dengan frekuensi harapan, kita harus memutuskan apakah ketaksesuaian itu kemungkinan besar disebabkan hanya oleh fluktuasi penarikan sampel, atau karena memang dadunya yang tidak setimbang, sehingga sebaran hasil percobaan menjadi tidak seragam.

Kita biasanya menyajikan setiap kemungkinan hasil percobaan itu dalam sel. Jadi, dalam ilustrasi ini, kita memiliki enam sel. Statistik yang dapat digunakan sebagai landasan kriteria keputusan bagi suatu percobaan yang melibatkan \(k\) sel didefinisikan sebagai berikut.

Bila frekuensi yang teramati sangat dekat dengan frekuensi harapannya, maka nilai \(χ^2\) akan kecil, yang mana menunjukkan adanya kesuaian yang baik. Bila frekuensi yang teramati berbeda cukup besar dari frekuensi harapannya, maka nilai \(χ^2\) akan besar sehingga kesuaiannya buruk. Kesuaian yang baik akan membawa pada penerimaan hipotesis nol \((H_0)\), sedangkan kesuaian yang buruk akan membawa pada penolakan \(H_0\).

Dengan demikian, wilayah kritisnya akan jatuh di ekor kanan sebaran chi-square nya. Untuk taraf nyata sebesar \(α\), nilai kritisnya \(χ_α^2\) dapat diperoleh dari Tabel Nilai Kritis Chi-Square. Jadi, wilayah kritisnya adalah \(χ^2>χ_α^2\). Kriteria keputusan yang diuraikan di sini hendaknya tidak digunakan bila ada frekuensi harapan yang kurang dari 5. Persyaratan ini mengakibatkan ada kalanya kita harus menggabungkan sel-sel yang berdekatan, sehingga mengakibatkan berkurangnya derajat bebas.

Dari Tabel 1 kita peroleh nilai \(χ^2\) nya sebesar

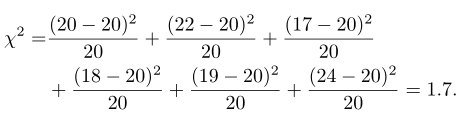
Dengan menggunakan Tabel Nilai Kritis Chi-Square, kita peroleh \(χ_{0,05}^2=11.070\) untuk \(v = 5\) derajat bebas. Karena \( χ^2 = 1.7\) lebih kecil daripada nilai kritisnya yakni 11.070, maka kita gagal untuk menolok \(H_0\), sehingga kita menyimpulkan bahwa sebarannya seragam. Dengan kata lain, dadu tersebut setimbang.

Sebagai gambaran kedua, marilah kita uji hipotesis bahwa sebaran frekuensi umur aki yang dicantumkan dalam Tabel 2 berikut dapat dihampiri dengan sebaran normal.

Tabel 2. Sebaran frekuensi relatif umur akir

Frekuensi harapan untuk setiap kelas (sel), yang dicantumkan dalam Tabel 3 di bawah, diperoleh dari kurva normal dengan nilai tengah dan simpangan yang sama dengan rata-rata dan simpangan baku sampel. Kita peroleh rata-rata sampel \(\overline{x}=3,5\) dan simpangan baku \(s = 0,7\).

Tabel 3. Frekuensi teramati dan harapan bagi umur aki di bawah asumsi kenormalan.

Kedua nilai itu akan digunakan sebagai \(μ\) dan \(σ\) untuk menghitung nilai-nilai \(z\) padanan batas-batas kelas. Sebagai misal, nilai \(z\) padanan batas kelas yang keempat adalah

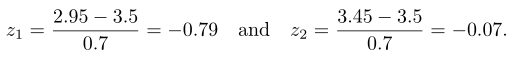
Dari Tabel Luas di bawah Kurva Normal, kita peroleh luas daerah \(z_1 = 0,79\) dan \(z_2 = 0,06\), yaitu

Dengan demikian, frekuensi harapan bagi kelas yang keempat adalah

Frekuensi harapan bagi selang kelas yang pertama sama dengan luas daerah di bawah kurva normal di sebelah kiri 1.95. Untuk selang kelas yang terakhir, kita gunakan luas daerah di sebelah kanan 4,45. Frekuensi harapan yang lain dapat diperoleh dengan menggunakan cara seperti yang digunakan bagi kelas yang keempat.

Perhatikan bahwa kita telah menggabungkan kelas-kelas yang berdekatn dalam Tabel 3, karena frekuensi harapannya kurang dari 5. Akibatnya, banyaknya selang berkurang dari 7 menjadi 4. Nilai \(χ^2\) dengan demikian diberikan oleh

Banyaknya derajat bebas bagi uji ini adalah 4 – 1 = 3, karena ada tiga besaran, yaitu frekuensi total, rata-rata dan simpangan baku, yang diperlukan untuk menghitung frekuensi-frekuensi harapan tersebut. Karena nilai \(χ^2\) hitung lebih kecil dari \(χ_{0,05}^2\) untuk 1 derajat bebas, maka tidak ada alasan untuk menolak hipotesis nol. Kita simpulkan bahwa sebaran normal memberikan kesuaian yang cukup baik bagi sebaran umur aki tersebut.

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.