Pendugaan Parameter Rata-rata Untuk Dua Populasi

Metode Statistika II » Pendugaan Parameter › Pendugaan Parameter Rata-rata Untuk Dua Populasi

Pendugaan Parameter

Pendugaan Parameter Rata-rata Untuk Dua Populasi

Bila kita mempunyai dua populasi dengan rata-rata \(μ_1\) dan \(μ_2\) dan varians \(σ_1^2\) dan \(σ_2^2\), maka penduga titik bagi selisih antara \(μ_1\) dan \(μ_2\) diberikan oleh statistik \(\overline{X}_1-\overline{X}_2\).

Oleh karena itu, untuk mendapatkan nilai dugaan titik bagi \(μ_1-μ_2\), kita mengambil dua sampel acak bebas, satu dari masing-masing populasi, yang berukuran \(n_1\) dan \(n_2\), dan kemudian menghitung selisih kedua rata-rata sampel \(\overline{x}_1-\overline{x}_2\).

Bila kedua sampel itu diambil dari populasi normal, atau bila \(n_1\) dan \(n_2\) keduanya lebih besar daripada 30, maka kita dapat memperoleh selang kepercayaan bagi \(μ_1-μ_2\) dengan mendasarkan pada distribusi sampling bagi \(\overline{X}_1-\overline{X}_2\).

Kita tahu bahwa distribusi sampling bagi \(\overline{X}_1-\overline{X}_2\) kira-kira akan menyebar normal dengan rata-rata dan simpangan baku sebagai berikut.

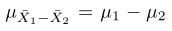
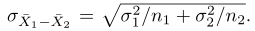
Dengan demikian, kita dapat menyatakan dengan peluang \(1-α\) bahwa peubah acak normal baku

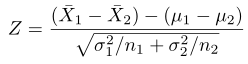
akan jatuh antara \(-z_{α/2}\) dan \(z_{α/2}\). Perhatikan Gambar 1 di bawah, kita peroleh

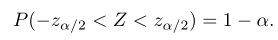
Gambar 1. \( P(-z_{α/2} < Z < z_{α/2}) = 1-α \)

Dengan mensubstitusikan \(Z\) kita mendapatkan bentuk ekivalennya, yakni

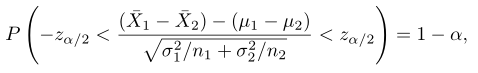
yang membawa pada selang kepercayaan \((1-α)100\)% bagi \(μ_1-μ_2\).

Selang Kepercayaan bagi \(μ_1-μ_2; σ_1^2 \, \text{dan} \, σ_2^2\) Diketahui.

Bila \(\overline{x}_1\) dan \(\overline{x}_2\) masing-masing adalah rata-rata sampel acak bebas berukuran \(n_1\) dan \(n_2\) yang diambil dari populasi dengan ragam \(σ_1^2\) dan \(σ_2^2\) yang diketahui, maka selang kepercayaan \((1-α)100\%\) bagi \(μ_1-μ_2\) adalah

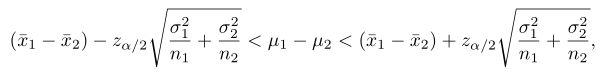
sedangkan dalam hal ini \(z_{α/2}\) adalah nilai peubah normal baku \(z\) yang luas daerah di sebelah kanannya sebesar \(α/2\).

Contoh 1:

Suatu ujian kimia diberikan pada 50 siswa perempuan dan 75 siswa laki-laki. Siswa-siswa perempuan mencapai rata-rata 76 dengan simpangan baku 6, sedangkan siswa-siswa laki-laki memperoleh rata-rata 82 dengan simpangan baku 8.

Tentukan selang kepercayaan 96% bagi beda \(μ_1-μ_2\), dalam hal ini \(μ_1\) adalah rata-rata skor semua siswa laki-laki dan \(μ_2\) adalah rata-rata skor semua siswa perempuan yang mungkin mengambil ujian ini.

Pembahasan:

Nilai dugaan titik bagi \(μ_1-μ_2\) adalah \(\overline{x}_1-\overline{x}_2=82-76=6\). Karena \(n_1\) dan \(n_2\) keduanya cukup besar, maka kita dapat mengganti \(σ_1\) dengan \(s_1=8\) dan \(σ_2\) dengan \(s_2=6\).

Dengan mengambil α = 0.04, kita memperoleh dari Tabel Normal bahwa \(z_{0.02}=2.05\). Dengan demikian, substitusi ke dalam rumus

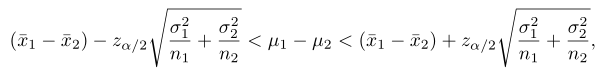
menghasilkan selang kepercayaan 96%-nya

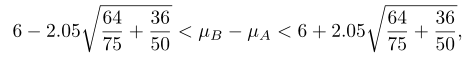
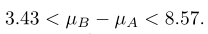
Selang Kepercayaan bagi \(μ_1-μ_2\) untuk sampel berukuran kecil; \(σ_1^2=σ_2^2\) tetapi Nilainya Tidak Diketahui.

Bila \(\overline{x}_1\) dan \(\overline{x}_2\) masing-masing adalah rata-rata sampel acak bebas berukuran \(n_1\) dan \(n_2\), yang diambil dari dua populasi yang hampir normal dengan ragam sama tetapi tidak diketahui nilainya, maka selang kepercayaan \((1-α )100\%\) bagi \(μ_1-μ_2\) diberikan oleh rumus

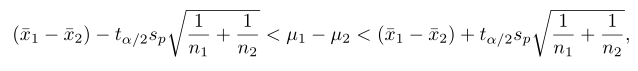
Sedangkan dalam hal ini \(s_p\) adalah nilai dugaan gabungan bagi simpangan baku populasi, dan \(t_{α/2}\) adalah nilai \(t\) dengan \(v=n_1+n_2-2\) derajat bebas yang luas daerah di sebelah kanannya sebesar \(α/2\).

Contoh 2:

Suatu pelajaran matematika diberikan pada 12 siswa dengan metode pengajaran yang biasa. Pelajaran yang sama diberikan pula pada 10 siswa tetapi dengan metode pengajaran yang menggunakan bahan yang telah diprogramkan.

Pada akhir semester setiap kelas diberikan ujian yang sama. Kelas yang pertama mencapai nilai rata-rata 85 dengan simpangan baku 4, sedangkan kelas yang kedua mencapai nilai rata-rata 81 dengan simpangan baku 5.

Tentukan selang kepercayaan 90% bagi selisih antara kedua rata-rata populasi, bila diasumsikan kedua populasi menyebar menghampiri normal dengan ragam yang sama.

Pembahasan:

Misalkan \(μ_1\) melambangkan rata-rata nilai semua siswa yang memperoleh pelajaran dengan metode pengajaran biasa dan \(μ_2\) melambangkan rata-rata nilai semua siswa yang memperoleh pelajaran yang menggunakan bahan terprogramkan.

Kita ingin membuat selang kepercayaan 90% bagi \(μ_1-μ_2\). Nilai dugaan titik bagi \(μ_1-μ_2\) adalah \(\overline{x}_1 - \overline{x}_2 = 85-81=4 \). Nilai dugaan gabungan, \(S_p^2\), bagi ragam \(σ^2\) dalam hal ini adalah

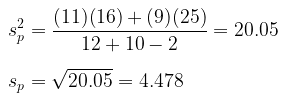
Dengan menggunakan α = 0.1, kita dapatkan dalam Tabel t bahwa \(t_{0.05} = 1.725\) untuk \(v=n_1+n_2-2=20\) derajat bebas. Oleh karena itu, selang kepercayaan 90% bagi \(μ_1-μ_2\) adalah

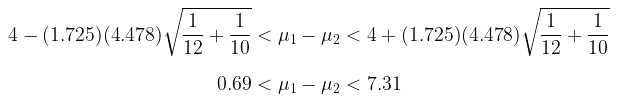
Jadi, kita percaya 90% bahwa selang dari 0.69 sampai 7.31 mencakup selisih sesungguhnya nilai rata-rata pelajaran matematika untuk kedua metode pengajaran tersebut. Kenyataan bahwa kedua ujung selang itu positif menunjukkan bahwa metode pengajaran biasa untuk pelajaran matematika ini lebih unggul daripada metode pengajaran dengan menggunakan bahan terprogramkan.

Selang Kepercayaan bagi \(μ_1-μ_2\) untuk sampel berukuran kecil; \(σ_1^2 ≠ σ_2^2\) dan Nilainya Tidak Diketahui

Bila \(\overline{x}_1\) dan \(s_1^2\), dan \(\overline{x}_2\) dan \(s_2^2\) masing-masing adalah rata-rata dan ragam sampel bebas berukuran kecil \(n_1\) dan \(n_2\) yang diambil dari dua populasi yang mendekati normal dengan ragam tidak sama dan tidak diketahui nilainya, maka selang kepercayaan \((1-α)100\%\) bagi \(μ_1-μ_2\), yang merupakan hampiran, diberikan oleh

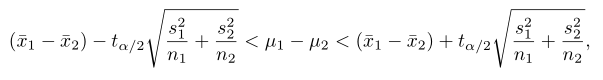
sedangkan dalam hal ini \(t_{α/2}\) adalah nilai t dengan berderajat bebas

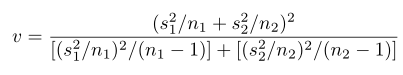
yang di sebelah kanannya terdapat daerah seluas α/2.

Contoh 3:

Catatan selama 15 tahun terakhir menunjukkan bahwa curah hujan rata-rata di suatu daerah selama bulan Mei adalah 4,93 sentimeter, dengan simpangan baku 1,14 sentimeter. Di daerah lain, catatan serupa selama 10 tahun terakhir menunjukkan bahwa curah hujan rata-rata di bulan Mei adalah 2,64 sentimeter dengan simpangan baku 0,66 sentimeter.

Tentukan selang kepercayaan 95% bagi selisih curah hujan rata-rata yang sebenarnya selama bulan Mei di kedua daerah tersebut, bila diasumsikan bahwa pengamatan-pengamatan itu berasal dari dua populasi normal dengan ragam yang berbeda.

Pembahasan:

Untuk daerah pertama kita mempunyai \(\overline{x}_1=4,93\,,s_1 = 1,14\,, \text{dan}\, n_1 = 15\); sedangkan untuk daerah yang kedua \(\overline{x}_1=2,64\,,s_2 = 0,66\,, \text{dan}\, n_2 = 10\). Kita ingin mendapatkan selang kepercayaan 96% bagi \(μ_1-μ_2\). Karena kedua ragam populasi dan ukurannya sampelnya tidak sama, maka kita hanya dapat memperoleh hampiran bagi selang kepercayaan 95% yang didasarkan pada sebaran t dengan derajat bebasnya yaitu

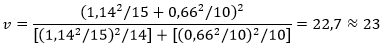
Nilai dugaan titik bagi \(μ_1-μ_2\) adalah \(\overline{x}_1 - \overline{x}_2 = 4,93-2,64=2,29\) . Dengan mengambil \(α=0,05\), kita mendapatkan dari Tabel t bahwa \(t_{0,025}=2,069\) untuk \(v=23\) derajat bebas. Dengan demikian, selang kepercayaan 95% bagi \(μ_1-μ_2\) adalah

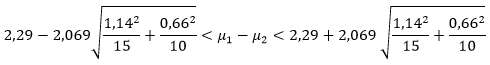
yang setelah disederhanakan menjadi

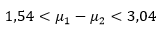
Dengan demikian, kita percaya 95% bahwa selisih curah hujan rata-rata yang sebenarnya selama bulan Mei di kedua daerah tersebut berada dalam selang dari 1,54 sampai 3,04 sentimeter.

Selang Kepercayaan bagi \(μ_D=μ_1-μ_2\) untuk Pengamatan Berpasangan

Bila \(\overline{d}\) dan \(s_d\) adalah rata-rata dan simpangan baku selisih n pengamatan berpasangan, maka selang kepercayaan \((1-α)100\%\) bagi \(μ_d=μ_1-μ_2\) adalah

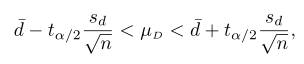
sedangkan dalam hal ini \(t_{α/2}\) adalah nilai t dengan \(v = n – 1\) derajat bebas yang luas daerah di sebelah kanannya \(α/2\).

Contoh 4:

Dua puluh mahasiswa tingkat satu dibagi ke dalam 10 pasang, setiap pasangan kira-kira mempunyai IQ yang sama. Salah seorang dari setiap pasangan diambil secara acak dan dimasukan ke dalam kelas yang hanya menggunakan bahan terprogramkan. Anggota pasangan yang lain dimasukkan ke dalam kelas biasa. Pada akhir semester kedua grup itu diberikan ujian yang sama dan hasilnya adalah sebagai berikut.

Tentukan selang kepercayaan 98% bagi selisih sesungguhnya dalam kedua metode pengajaran tersebut.

Pembahasan:

Kita ingin mendapatkan selang kepercayaan 98% bagi \(μ_1-μ_2\), sedangkan \(μ_1\) dan \(μ_2\) adalah nilai rata-rata semua siswa yang mungkin mengikuti kuliah dengan bahan terprogramkan dan kuliah biasa. Karena pengamatannya berpasangan, \(μ_1-μ_2=μ_D\), dan nilai dugaan titik bagi \(μ_D\) diberikan oleh \(\overline{d} = -1,6\). Ragam selisih-selisih tersebut adalah

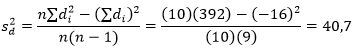
Dengan mengakarkan kita peroleh \(s_d=6,38\). Untuk \(α=0,02\), kita peroleh dari Tabel t bahwa \(t_{0,01}=2,821\) untuk v=n-1=9 derajat bebas. Dengan demikian, selang kepercayaan 98% bagi \(μ_D\) adalah

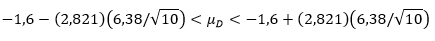
yang setelah disederhanakan menjadi

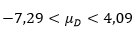
Dengan demikian, kita percaya 98% bahwa selang dari -7,29 sampai 4,09 mencakup selisih nilai rata-rata yang sebenarnya bagi kedua metode pengajaran tersebut. Karena selang ini memungkinkan nilai \(μ_D\) sama dengan nol, maka kita tidak dapat menyimpulkan bahwa metode pengajaran yang satu lebih baik daripada metode pengajaran lainnya, meskipun untuk sampel yang diperoleh ini metode pengajaran biasa menunjukkan hasil yang lebih baik.

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

METODE STATISTIKA II

Metode Statistika II » Pendugaan Parameter › Pendugaan Parameter Rata-rata Untuk Dua Populasi

Pendugaan Parameter