
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Uji Normalitas › Normal Probability Plot
Normalitas
Normal Probability Plot
Normal Probability Plot sering diaplikasikan dalam analisis regresi untuk pemeriksaan asumsi normalitas yakni untuk mengidentifikasi apakah galat atau kesalahan acak berdistribusi normal atau tidak.
Normal Probability Plot (NPP) sering diaplikasikan dalam analisis regresi untuk pemeriksaan asumsi normalitas yakni untuk mengidentifikasi apakah galat atau kesalahan acak (random error) berdistribusi normal atau tidak.
Terdapat beberapa tahapan untuk memeriksa kenormalan peubah acak menggunakan normal probability plot. Kita jelaskan beberapa tahapan tersebut dalam contoh berikut.
Misalnya pada kasus regresi linier sederhana antara \(y\) (IPK) terhadap \(x\) (skor tes masuk perguruan tinggi) dari 20 observasi sebagai berikut:
| \(i\) | Skor Test (\(X\)) | IPK (\(Y\)) |
|---|---|---|
| 1 | 4.7 | 1.5 |
| 2 | 4.3 | 1.4 |
| 3 | 5.0 | 2.0 |
| 4 | 4.9 | 2.0 |
| 5 | 6.3 | 3.2 |
| 6 | 4.6 | 1.8 |
| 7 | 4.3 | 1.6 |
| 8 | 5.0 | 2.3 |
| 9 | 5.2 | 2.6 |
| 10 | 4.8 | 2.3 |
| 11 | 6.0 | 3.4 |
| 12 | 5.4 | 2.9 |
| 13 | 5.5 | 3.1 |
| 14 | 6.2 | 3.7 |
| 15 | 3.9 | 1.9 |
| 16 | 4.5 | 2.5 |
| 17 | 4.1 | 2.2 |
| 18 | 5.9 | 3.8 |
| 19 | 4.7 | 2.8 |
| 20 | 4.7 | 3.0 |
Tahapan-tahapan untuk membuat normal probability plot, yaitu
Langkah 1: Regresikan \(y\) terhadap \(x\).
Dari hasil regresi diperoleh hasil sebagai berikut:
\[\hat{y_i}=-1,6995+0,8399x_i \]
\[MSE=s^2=0,1892\]
Langkah 2: Hitung nilai residual, lalu diurutkan dari yang terkecil ke yang terbesar.
| \(i\) | Skor Test (\(X\)) | IPK (\(Y\)) | \(\hat{Y_i}\) | \(e_i\) |
|---|---|---|---|---|
| 1 | 4.7 | 1.5 | 2.25 | -0.75 |
| 2 | 4.3 | 1.4 | 1.91 | -0.51 |
| 3 | 5.0 | 2.0 | 2.50 | -0.50 |
| 4 | 4.9 | 2.0 | 2.42 | -0.42 |
| 5 | 6.3 | 3.2 | 3.59 | -0.39 |
| 6 | 4.6 | 1.8 | 2.16 | -0.36 |
| 7 | 4.3 | 1.6 | 1.91 | -0.31 |
| 8 | 5.0 | 2.3 | 2.50 | -0.20 |
| 9 | 5.2 | 2.6 | 2.67 | -0.07 |
| 10 | 4.8 | 2.3 | 2.33 | -0.03 |
| 11 | 6.0 | 3.4 | 3.34 | 0.06 |
| 12 | 5.4 | 2.9 | 2.84 | 0.06 |
| 13 | 5.5 | 3.1 | 2.92 | 0.18 |
| 14 | 6.2 | 3.7 | 3.51 | 0.19 |
| 15 | 3.9 | 1.9 | 1.58 | 0.32 |
| 16 | 4.5 | 2.5 | 2.08 | 0.42 |
| 17 | 4.1 | 2.2 | 1.74 | 0.46 |
| 18 | 5.9 | 3.8 | 3.26 | 0.54 |
| 19 | 4.7 | 2.8 | 2.25 | 0.55 |
| 20 | 4.7 | 3.0 | 2.25 | 0.75 |
Langkah 3: Cari nilai harapan dari residual yang telah diurutkan tersebut di bawah asumsi kenormalan.
Teori statistik mengatakan bahwa untuk peubah acak (random variables) dengan rata-rata 0 dan estimasi variannya MSE, maka pendekatan yang baik untuk nilai harapan dari observasi terkecil ke-i dalam suatu sampel acak (random samples) berukuran \(n\) adalah
\[\sqrt{MSE} \left[z \frac{i-0,375}{n+0,25} \right] \]
di mana \(z(A)\) merupakan persentile ke-\(A\) dari distribusi normal baku.
| i | Skor Test (X) | IPK (Y) | \(\hat{Y_i}\) | \(e_i\) | \(\frac{1-0,375}{n+0,25} \) | \(z \left(\frac{1-0,375}{n+0,25} \right)\) | \(\sqrt{MSE} z \left(\frac{1-0,375}{n+0,25} \right)\) |
|---|---|---|---|---|---|---|---|
| 1 | 4.7 | 1.5 | 2.25 | -0.75 | 0.03 | -1.87 | -0.81 |
| 2 | 4.3 | 1.4 | 1.91 | -0.51 | 0.08 | -1.40 | -0.61 |
| 3 | 5.0 | 2.0 | 2.50 | -0.50 | 0.13 | -1.13 | -0.49 |
| 4 | 4.9 | 2.0 | 2.42 | -0.42 | 0.18 | -0.92 | -0.40 |
| 5 | 6.3 | 3.2 | 3.59 | -0.39 | 0.23 | -0.74 | -0.32 |
| 6 | 4.6 | 1.8 | 2.16 | -0.36 | 0.28 | -0.59 | -0.26 |
| 7 | 4.3 | 1.6 | 1.91 | -0.31 | 0.33 | -0.45 | -0.19 |
| 8 | 5.0 | 2.3 | 2.50 | -0.20 | 0.38 | -0.31 | -0.14 |
| 9 | 5.2 | 2.6 | 2.67 | -0.07 | 0.43 | -0.19 | -0.08 |
| 10 | 4.8 | 2.3 | 2.33 | -0.03 | 0.48 | -0.06 | -0.03 |
| 11 | 6.0 | 3.4 | 3.34 | 0.06 | 0.52 | 0.06 | 0.03 |
| 12 | 5.4 | 2.9 | 2.84 | 0.06 | 0.57 | 0.19 | 0.08 |
| 13 | 5.5 | 3.1 | 2.92 | 0.18 | 0.62 | 0.31 | 0.14 |
| 14 | 6.2 | 3.7 | 3.51 | 0.19 | 0.67 | 0.45 | 0.19 |
| 15 | 3.9 | 1.9 | 1.58 | 0.32 | 0.72 | 0.59 | 0.26 |
| 16 | 4.5 | 2.5 | 2.08 | 0.42 | 0.77 | 0.74 | 0.32 |
| 17 | 4.1 | 2.2 | 1.74 | 0.46 | 0.82 | 0.92 | 0.40 |
| 18 | 5.9 | 3.8 | 3.26 | 0.54 | 0.87 | 1.13 | 0.49 |
| 19 | 4.7 | 2.8 | 2.25 | 0.55 | 0.92 | 1.40 | 0.61 |
| 20 | 4.7 | 3.0 | 2.25 | 0.75 | 0.97 | 1.87 | 0.81 |
Langkah 4: Buat scatter-plot antara residual \((e_i)\) dan nilai harapan di bawah kenormalan \(\sqrt{MSE} \left[z \frac{i-0,375}{n+0,25} \right] \).
Jika plot memiliki kecenderungan mengikuti garis lurus, maka data (error) mengikuti distribusi normal. Dari hasil pengolahan diperoleh hasil sebagai berikut:
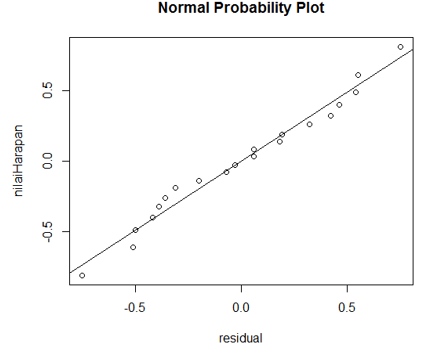
Dari grafik di atas dapat dilihat bahwa plot memiliki kecenderungan mengikuti garis lurus. Dengan demikian, data (error) dapat dikatakan mengikuti distribusi normal.
Artikel Terkait
Attitude is a little thing that makes a big difference.
Winston Churchill