
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pengujian Hipotesis › Uji Hipotesis Rata-Rata Dua Populasi
Pengujian Hipotesis
Uji Hipotesis Rata-Rata Dua Populasi
Suatu penelitian sering kali menggunakan dua sampel atau lebih sebagai objek penelitiannya. Tujuannya adalah untuk melihat ada-tidaknya perbedaan setelah sampel-sampel tersebut diberi perlakuan berbeda.
Suatu penelitian sering kali menggunakan dua sampel atau lebih sebagai objek penelitiannya. Tujuannya adalah untuk melihat ada-tidaknya perbedaan setelah sampel-sampel tersebut diberi perlakuan berbeda. Untuk itu, dilakukan pengujian hipotesis rata-rata dua populasi.
Terdapat beberapa kondisi yang perlu diperhatikan dalam pengujian hipotesis rata-rata dua populasi yakni ketika varians sama dan diketahui, varians sama dan tidak diketahui, varians tidak sama dan tidak diketahui, serta kondisi untuk pengamatan berpasangan.
Varians Sama dan Diketahui
Misalkan dua sampel acak independen masing-masing dengan ukuran \(n_1\) dan \(n_2\) ditarik dari populasi dengan rata-rata \(μ_1\) dan \(μ_2\) dan varians \(σ_1^2\) dan \(σ_2^2\). Kita tahu bahwa peubah acak
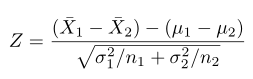
mempunyai distribusi normal standard. Di sini kita mengasumsikan bahwa \(n_1\) dan \(n_2\) cukup besar sehingga Teorema Limit Pusat (Central Limit Theorem) berlaku. Tentu saja, jika dua populasi tersebut berdistribusi normal, maka statistik di atas akan berdistribusi normal bahkan untuk \(n_1\) dan \(n_2\) yang kecil. Selain itu, jika kita bisa mengasumsikan bahwa \(σ_1=σ_2=σ\), maka statistik di atas menjadi
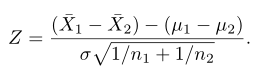
Dua statistik di atas menjadi dasar untuk pengembangan prosedur uji yang melibatkan dua rata-rata. Hipotesis nol untuk selisih dua rata-rata bisa dituliskan sebagai

Tentu saja, hipotesis alternatifnya bisa berupa dua arah atau satu arah, yakni

Jadi, untuk uji hipotesis dua rata-rata dengan variansnya diketahui, kita menghitung nilai \(\overline{x}_1\) dan \(\overline{x}_2\), lalu menggunakan statistik uji berikut

Untuk uji dua arah, maka kita tolak Ho dan menerima \(H_1:μ_1-μ_2≠d_0\) apabila \(z>z_{α/2}\) atau \(z<-z_{α/2}\). Sedangkan untuk uji satu arah maka kita tolak Ho dan menerima \(H_1:μ_1-μ_2>d_0\) apabila \(z>z_α\) dan menerima \(H_1:μ_1-μ_2 < d_0\) apabila \(z < z_α\). Kita nyatakan ini dalam tabel berikut.
Tabel 1. Pengujian hipotesis rata-rata dua populasi untuk varians sama dan diketahui

Varians Sama Tetapi Tidak Diketahui
Jika kita dapat mengasumsikan bahwa kedua populasi adalah berdistribusi normal dan bahwa \(σ_1=σ_2=σ\), maka uji-t gabungan (pooled t-test) dapat digunakan. Kita nyatakan ini lebih lanjut dalam definisi berikut.
Definisi:
Untuk hipotesis dua arah
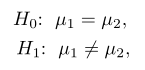
Kita tolak Ho pada tingkat signifikansi \(α\) ketika statistik hitung

di mana

lebih besar dari \(t_{α/2;n_1+n_2-2}\) atau kurang dari \(-t_{α/2;n_1+n_2-2}\).
Hipotesis, statistik uji dan wilayah kritis penolakannya untuk pengujian hipotesis rata-rata dua populasi di mana varians sama dan tak diketahui dinyatakan dalam tabel berikut.
Tabel 2. Pengujian hipotesis rata-rata dua populasi untuk varians sama tetapi tidak diketahui

Contoh Soal:
Sebuah pelajaran matematika diberikan pada 12 siswa dengan metode pengajaran yang biasa. Kelas lain yang terdiri atas 10 siswa diberi pelajaran yang sama tetapi dengan metode yang menggunakan bahan yang telah terprogramkan.
Pada akhir semester murid kedua kelas itu diberikan ujian yang sama. Kelas pertama mencapai nilai rata-rata 85 dengan simpangan baku 4, sedang kelas yang menggunakan bahan yang terprogramkan memperoleh nilai rata-rata 81 dengan simpangan baku 5.
Ujilah hipotesis bahwa kedua metode mengajar matematika itu sama, dengan menggunakan taraf nyata 0,10. Asumsikan bahwa kedua populasi itu menghampiri sebaran normal dengan ragam yang sama.
Pembahasan:
Misalkan \(μ_1\) dan \(μ_2\) adalah nilai rata-rata semua siswa yang mungkin mengambil pelajaran tersebut dengan kedua cara mengajar. Dengan menggunakan langkah-langkah dalam prosedur pengujian hipotesis, kita peroleh
- \(H_0:μ_1=μ_2\) atau \(μ_1-μ_2=0\).
- \(H_1:μ_1≠μ_2\) atau \(μ_1-μ_2≠0\).
- \(α=0,10\).
- Wilayah kritis: \(t<-1,725\) atau \(t>1,725\), sedangkan dalam hal ini
- Perhitungan:
- Keputusan: Tolak Ho dan simpulkan bahwa kedua metode mengajar tidak sama. Karena nilai t hitung jatuh di wilayah kritik bagian kanan, kita dapat menyimpulkan bahwa metode mengajar biasa lebih baik daripada metode dengan bahan terprogramkan.
dengan \(v = 20\) derajat bebas.


Dengan demikian

Varians Tidak Sama dan Tidak DiKetahui
Terdapat situasi di mana kita tidak dapat mengasumsikan bahwa \(σ_1=σ_2\). Jika dua populasi adalah normal, maka statistik

akan mendekati distribusi-t dengan derajat bebas
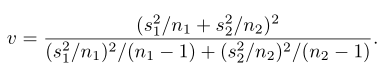
Akibatnya, prosedur pengujian tidak menolak Ho ketika

Hipotesis, statistik uji dan wilayah kritis penolakannya untuk pengujian hipotesis rata-rata dua populasi di mana varians tak sama dan tak diketahui dinyatakan dalam tabel berikut.
Tabel 3. Pengujian hipotesis rata-rata dua populasi untuk varians tidak sama dan tidak diketahui

Pengamatan Berpasangan
Pengujian dua rata-rata bisa dicapai saat data dalam bentuk pengamatan berpasangan. Dalam struktur berpasangan ini, kondisi dua populasi (perlakuan) ditetapkan secara acak di dalam unit yang homogen. Penghitungan selang kepercayaan bagi \(μ_1-μ_2\) dalam situasi dengan pengamatan berpasangan di dasarkan pada peubah acak

di mana \(\overline{D}\) dan \(S_d\) adalah peubah-peubah acak yang menyatakan rata-rata dan standar deviasi perbedaan pengamatan dalam unit percobaan. Seperti dalam kasus pooled t-test, asumsinya adalah pengamatan dari tiap populasi berdistribusi normal.
Masalah dua-sampel ini secara esensi direduksi menjadi masalah satu-sampel dengan menggunakan perbedaan hitung (computed differences) \(d_1,d_2,…,d_n\). Oleh karena itu, hipotesis direduksi menjadi

Statistik uji hitung kemudian diberikan oleh

Wilayah kritis dibangun dengan menggunakan distribusi t dengan n – 1 derajat bebas.
Hipotesis, statistik uji dan wilayah kritis penolakannya untuk pengujian hipotesis rata-rata dua pengamatan berpasangan (paired observations) dinyatakan dalam tabel berikut.
Tabel 4. Pengujian hipotesis rata-rata dua pengamatan berpasangan

Contoh soal:
Untuk mengetahui apakah keanggotaan dalam organisasi mahasiswa mempunyai akibat baik atau buruk pada nilai seseorang, nilai mutu rata-rata berikut ini telah dikumpulkan selama periode 5 tahun;

Dengan mengasumsikan bahwa populasinya normal, ujilah pada taraf nyata 0,025 apakah keanggotaan dalam organisasi mahasiswa berakibat buruk pada nilai yang dicapai seseorang.
Pembahasan:
Misalkan \(μ_1\) dan \(μ_2\) masing-masing adalah nilai mutu rata-rata bagi siswa anggota dan bukan anggota organisasi mahasiswa. Dengan mengikuti langkah-langkah dalam prosedur pengujian hipotesis, diperoleh
- \(H_0:μ_1=μ_2\) atau \(μ_D=μ_1-μ_2=0\).
- \(H_1:μ_1<μ_2\) atau \(μ_D=μ_1-μ_2<0\).
- \(α=0,025\).
- Wilayah kritik: \(t<-2,776\), yang dalam hal ini
- Perhitungan:
- Keputusan: Terima Ho dan simpulkan bahwa keanggotaan organisasi bagi mahasiswa tidak memberikan pengaruh yang berarti pada nilai yang dicapainya.
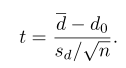
dengan \(v = 4\) derajat bebas.

Kita peroleh \(\overline{d}=-0,5/5=-0,1\) dan

Dengan mengambil akarnya kita memperoleh \(s_d=0,14142\). Dengan demikian,

Artikel Terkait
On every thorn, delightful wisdom grows. In every rill a sweet instruction flows.
Edward Young