
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Uji Normalitas › Uji Kolmogorov-Smirnov
Normalitas
Uji Kolmogorov-Smirnov
Uji Kolmogorov-Smirnov termasuk dalam kategori goodness of fit test, yakni suatu uji untuk mengetahui apakah suatu data mengikuti distribusi teoritis tertentu (misalnya apakah berdistribusi normal atau poisson).
Uji Kolmogorov-Smirnov merupakan salah satu uji untuk memeriksa kenormalan suatu peubah acak. Uji ini termasuk dalam kategori goodness of fit test, yakni suatu uji untuk mengetahui apakah suatu data mengikuti distribusi teoritis tertentu (misalnya apakah berdistribusi normal atau poisson).
Tahapan Uji Kolmogov-Smirnov
Untuk melakukan pengujian normalitas dengan uji kolmogorov-smirnov, kita dapat mengikuti beberapa langkah berikut:
- Tentukan hipotesis
- Tentukan tingkat signifikansi
- Menghitung statistik uji
- Wilayah kritis:
- Keputusan: Tolak Ho pada suatu taraf nyata tertentu jika uji statistik \(D\) melebihi \(α\) yang ditunjukkan pada tabel kolmogorov-smirnov.
- Kesimpulan
Ho: Populasi mengikuti distribusi normal
H1: Populasi tidak mengikuti distribusi normal
\[ D = \max |F(x)-S(x)| \]
\(D =\) nilai tertinggi dari perbedaan antara \(S(x)\) dan \(F(x)\)
Untuk mendapatkan gambaran yang lebih jelas, perhatikanlah contoh berikut.
Contoh 1:
Diberikan data berat dari 36 ginjal kelinci yang akan dilakukan eksperimen sebagai berikut.
| 58 | 78 | 84 | 90 | 97 | 70 | 90 | 86 | 82 |
| 59 | 90 | 70 | 74 | 83 | 90 | 76 | 88 | 84 |
| 68 | 93 | 70 | 94 | 70 | 110 | 67 | 68 | 75 |
| 80 | 68 | 82 | 104 | 92 | 112 | 84 | 98 | 80 |
Ujilah apakah sampel berasal dari distribusi normal dengan rata-rata 85 gram dan standar deviasi 15 gram (taraf nyata 5%).
Pembahasan:
- Menentukan hipotesis
- Tingkat signifikansi yang digunakan 0,05 (α=5%)
- Menghitung statistik uji:
- Keputusan: Tidak tolak Ho, karena \(D < 0,2219\) (Tabel Kolmogorov-Smirnov)
- Kesimpulan: Dengan tingkat signifikansi 5% kita simpulkan bahwa data sampel berasal dari distribusi normal dengan \(\mu = 85\) dan \(σ=15\).
Ho: Populasi mengikuti distribusi normal
H1: Populasi tidak mengikuti distribusi normal
Menghitung S(x)

Menghitung F(x):
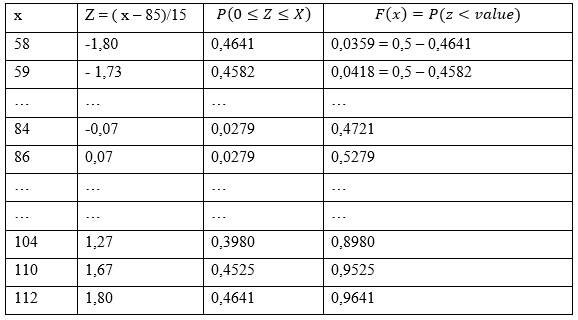
Menghitung \(F(x) – S(x)\)
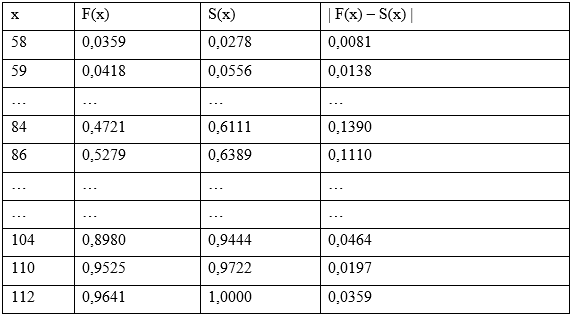
\[ D=maks |F(x)-S(x)|=0,1390=0,14 \]
Catatan: Ketika uji Kolmogorov-Smirnov digunakan untuk menguji hipotesis bahwa sampel diambil dari suatu populasi dengan parameter yang tidak diketahui, maka uji Kolmogorov-Smirnov kurang baik hasilnya.
Untuk alasan tersebut, sebuah pengujian telah dikembangkan yang dikenal dengan uji Liliefors di mana dalam pengujian tersebut informasi parameter rata-rata \((\mu)\) dan varians \((σ^2)\) tidak diketahui dan untuk itu perlu dilakukan estimasi dari data sampel.
Artikel Terkait
Jika kamu kehilangan seseorang, tapi menemukan dirimu yang sebenarnya, kamu menang.
Paulo Coelho