
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pengujian Hipotesis › Uji Hipotesis Ragam Satu Populasi
Pengujian Hipotesis
Uji Hipotesis Ragam Satu Populasi
Selain pengujian hipotesis terhadap rata-rata dan proporsi, kita juga dapat melakukan pengujian hipotesis mengenai keragaman suatu populasi atau membandingkan keragaman suatu populasi dengan keragaman populasi lainnya.
Selain pengujian hipotesis terhadap rata-rata dan proporsi, kita juga dapat melakukan pengujian hipotesis mengenai keragaman suatu populasi atau membandingkan keragaman suatu populasi dengan keragaman populasi lainnya.
Misalnya, kita ingin menguji hipotesis bahwa keragaman persentase ketakmurnian suatu zat tidak melebihi batas yang dibolehkan, atau keragaman umur cat tembok tertentu sama dengan keragaman umur cat tembok lain yang merupakan saingannya.
Pertama-tama marilah kita perhatikan pengujian hipotesis nol \(H_0\) bahwa varians populasi \(σ^2\) sama dengan nilai tertentu \(σ_0^2\) lawan salah satu dari alternatif \(σ^2<σ_0^2, σ^2>σ_0^2\), atau \(σ^2≠σ_0^2\). Statistik uji yang digunakan sebagai landasan keputusan adalah peubah acak chi-square.
Bila sebaran populasi yang diambil sampelnya sekurang-kurangnya menghampiri normal, nilai chi-square bagi pengujian \(σ^2=σ_0^2\) diberikan menurut rumus

di mana n adalah ukuran sampel, \(s^2\) adalah ragam sampel, dan \(σ_0^2\) adalah nilai \(σ^2\) menurut hipotesis nol. Bila \(H_0\) benar, \(χ^2\) adalah nilai sebaran chi-square dengan \(v = n -1\) derajat bebas.
Jadi, untuk uji dua-arah pada taraf nyata \(α\), wilayah kritisnya adalah \(χ^2<χ_{1-α/2}^2\) dan \(χ^2>χ_{α/2}^2\). Bila alternatifnya satu-arah \(σ^2<σ_0^2\), maka wilayah kritisnya adalah \(χ^2<χ_{1-α}^2\), sedangkan bila alternatifnya adalah \(σ^2>σ_0^2\), maka wilayah kritisnya adalah \(χ^2>χ_α^2\).
Contoh 1:
Sebuah perusahaan aki mobil mengatakan bahwa umur aki yang diproduksinya mempunyai simpangan baku 0,9 tahun. Bila suatu sampel acak 10 aki menghasilkan simpangan baku \(s = 1,2\) tahun, apakah menurut Anda \(σ>0,9\) tahun? Gunakan taraf nyata 0,05.
Pembahasan:
- \(H_0:σ^2=0,81\)
- \(H_1:σ^2>0,81\)
- \(α=0,05\).
- Wilayah kritik: Hipotesis nol akan ditolak bila \(χ^2>16,919\)
- Perhitungan: \(s^2=1,44, n=10\), dan
- Keputusan: Terima Ho dan simpulkan bahwa tidak ada alasan untuk meragukan bahwa simpangan bakunya adalah 0,9 tahun.
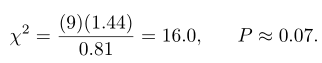
Contoh 2:
Diketahui \(σ\) dari lama pembuatan suatu masakan adalah 40 menit. Jika sampel acak sebanyak 25 dari lama pembuatan suatu masakan dengan resep baru memiliki standar deviasi sebesar 25, tentukan apakah \(σ\) dari resep baru kurang dari resep lama! \((α=0,05)\).
Pembahasan:
- \(H_0:σ^2=1600\)
- \(H_1:σ^2<1600\)
- \(α=0,05\)
- Wilayah kritik: Hipotesis nol akan ditolak bila \(χ^2 < χ_{1-α/2}^2\) atau \(χ^2 < χ_{0,95; 24}^2 = 13,848\)
- Perhitungan: n = 25, \(σ = 40\), s = 25
- Keputusan: Tolak Ho karena \(χ^2 < χ_{1-α/2}^2\) yaitu \(9,375 < 13,848\)
- Kesimpulan: Dengan tingkat signifikansi 5%, dapat disimpulkan bahwa lama pembuatan masakan resep baru kurang dari 40 menit.
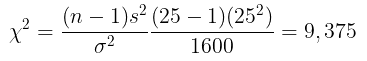
Artikel Terkait
It’s not the load that weighs you down, it’s how you carry it.
C.S. Lewis