Metode Statistika II   »   Pengujian Hipotesis   ›  Uji Hipotesis Proporsi Satu Populasi

Pengujian Hipotesis

Uji Hipotesis Proporsi Satu Populasi

Uji hipotesis mengenai proporsi diperlukan di banyak bidang, misalnya seorang politikus ingin mengetahui berapa proporsi pemilih yang akan memilih partainya dalam pemilu mendatang.

---

Uji hipotesis mengenai proporsi diperlukan di banyak bidang. Misalnya seorang politikus tentu ingin mengetahui berapa proporsi pemilih yang akan memilih partainya dalam pemilihan umum mendatang. Semua pabrik sangat berkepentingan mengetahui proporsi barang yang cacat selama pengiriman. Seorang penjudi tentu sangat bergantung pada pengetahuan mengenai proporsi hasil yang ia anggap menguntungkan.

Pada artikel ini kita akan membahas masalah pengujian hipotesis bahwa proporsi keberhasilan dalam suatu percobaan binomial sama dengan suatu nilai tertentu. Artinya, kita akan menguji hipotesis \(H_0\) bahwa \(p=p_0\), sedangkan \(p\) adalah parameter sebaran binomial. Hipotesis alternatifnya dapat berupa satu-arah atau dua-arah: \(p < p_0, p>p_0\), atau \(p≠p_0\).

Statistik yang akan kita gunakan sebagai landasan kriterium keputusan adalah peubah acak binomial \(X\), meski kita pun dapat menggunakan statistik \(\overline{P}=X/n\) sama baiknya. Nilai-nilai \(X\) yang jauh dari rata-rata \(μ=np_0\) akan membawa pada penolakan hipotesis nol.

Untuk menguji hipotesis

kita gunakan distribusi binomial untuk menghitung nilai-P, yakni

Nilai x menyatakan banyaknya sukses dalam sampel berukuran n. Bila nilai-P ini lebih kecil atau sama dengan α, uji kita signifikan pada taraf α dan kita tolak Ho dan menerima H1. Begitu pula, untuk menguji

pada tingkat signifikansi α, hitunglah

dan tolak Ho dan menerima H1 bila nilai-P lebih kecil atau sama dengan α.

Terakhir, untuk menguji

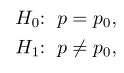
pada tingkat signifikansi α, hitunglah

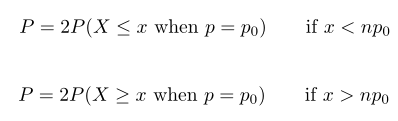
dan tolak Ho dan menerima H1 bila nilai-P hitung lebih kecil atau sama dengan α.

Langkah-langkah untuk pengujian hipotesis nol mengenai proporsi lawan berbagai hipotesis alternatifnya dengan menggunakan peluang binomial pada Tabel Binomial adalah sebagai berikut:

1. \(H_0:p=p_0\).
2. \(H_1\): Alternatifnya adalah \(p < p_0, p>p_0\), atau \(p≠p_0\).
3. Tentukan tingkat signifikansi α.
4. Statistik uji: Peubah Binomial \(X\) dengan \(p=p_0\)
5. Perhitungan: Hitunglah \(x\), yaitu banyaknya keberhasilan. Kemudian hitung nilai-P yang sesuai.
6. Keputusan: Tariklah kesimpulan berdasarkan nilai-P.

Dari Contoh 1, kita mengetahui bahwa nilai-nilai peluang binomial dapat dihitung langsung dari rumus binomial dari Tabel Binomial bila n kecil. Untuk n yang besar kita dapat menggunakan prosedur hampiran (approximation). Bila nilai yang dihipotesiskan \(p_0\) mendekati nol atau 1, kita dapat menggunakan sebaran Poisson dengan parameter \(μ=np_0\).

Namun, untuk n yang besar, hampiran normal dengan parameter \(μ=np_0\) dan \(σ^2=np_o q_0\) biasanya lebih disukai, dan hampiran ini memang sangat teliti asalkan \(p_0\) tidak terlalu mendekati pada nol atau 1. Bila digunakan hampiran normal, nilai \(z\) untuk pengujian \(p=p_0\) diberikan oleh

\[ z = \frac{p-p_0}{\sqrt{pq/n}} \]

yang merupakan nilai bagi peubah acak normal baku \(Z\). Oleh karena itu, untuk uji dua-arah dengan taraf nyata α, wilayah kritisnya adalah \(z < -z_{α/2}\) dan \(z > z_{α/2}\). Bila alternatifnya satu-arah \(p < p_0\), wilayah kritisnya adalah \(z<-z_α\), dan bila alternatifnya \(p>p_0\), maka wilayah kritisnya \(z>z_α\).

Untuk menguji hipotesis nol mengenai proporsi populasi dengan menggunakan hampiran normal, kita menggunakan langkah-langkah sebagai berikut:

1. \(H_0:p=p_0\).
2. \(H_1\): Alternatifnya adalah \(p < p_0, p>p_0\), atau \(p≠p_0\).
3. Tentukan tingkat signifikansi α.
4. Perhitungan: Dari sampel berukuran n yang diperoleh, hitunglah x dan kemudian
5. Wilayah kritisnya: \(z<-z_α\) bila alternatifnya \(p < p_0, z>z_α\) bila alternatifnya \(p>p_0, z<-z_{α/2}\) dan \(z>z_{α/2}\) bila alternatifnya \(p≠p_0\).
6. Keputusan: Tolak Ho bila \(z\) jatuh ke dalam wilayah kritis; dan terima Ho bila \(z\) jatuh ke dalam wilayah penerimaan.