
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pengujian Hipotesis › Uji Hipotesis Rata-Rata Satu Populasi
Pengujian Hipotesis
Uji Hipotesis Rata-Rata Satu Populasi
Terdapat dua kondisi yang perlu diperhatikan dalam pengujian hipotesis rata-rata satu populasi yakni ketika varians dari populasi diketahui dan ketika varians populasi tidak diketahui.
Pada artikel ini kita akan membahas pengujian hipotesis untuk rata-rata satu populasi. Terdapat dua kondisi yang perlu diperhatikan yakni ketika varians dari populasi diketahui (variance known) dan ketika varians populasi tidak diketahui (variance unknown).
Varians Diketahui (Variance Known)
Misalkan diberikan suatu populasi yang variansnya \(σ^2\) diketahui. Sekarang kita ingin menguji hipotesis bahwa rata-rata populasinya \(μ\) sama dengan nilai tertentu \(μ_0\) lawan hipotesis alternatifnya bahwa rata-rata populasinya itu tidak sama dengan \(μ_0\). Dengan kata lain, kita ingin menguji:
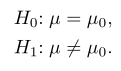
Statistik uji yang dapat digunakan dalam hal ini adalah peubah acak \(\overline{X}\). Dengan mengambil tingkat signifikansi sebesar \(α\), kita dapat menemukan dua nilai kritis \(\overline{x}_1\) dan \(\overline{x}_2\) sedemikian sehingga \(\overline{x}_1≤\overline{x}≤\overline{x}_2\) merupakan wilayah penerimaan, dan kedua ekor sebarannya, \(\overline{x} < \overline{x}_1\) dan \(\overline{x} > \overline{x}_2\), menyusun wilayah kritisnya.
Perhatikan bahwa kita biasanya melakukan transformasi \(\overline{X}\) ke dalam bentuk statistik uji \(Z\) sehingga nilai kritis itu dapat dinyatakan dalam nilai \(z\) melalui transformasi berikut:
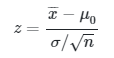
Dengan demikian, untuk tingkat signifikansi sebesar \(α\), kedua nilai kritis \(z\) padanan bagi \(\overline{X}_1\) dan \(\overline{X}_2\), yakni (perhatikan Gambar 1)
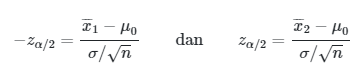
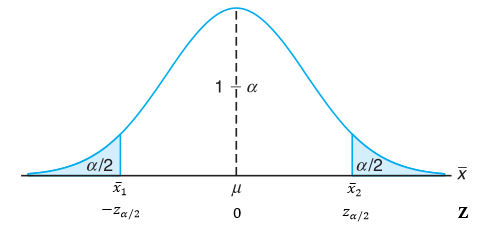
Gambar 1
Jadi, dari populasi tersebut diambil sebuah sampel acak berukuran \(n\) dan dihitung rata-rata sampelnya \(\overline{x}\). Bila \(\overline{x}\) jatuh dalam wilayah penerimaan \(\overline{x}_1≤\overline{x}≤\overline{x}_2\), maka
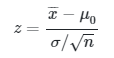
akan jatuh dalam wilayah \(-z_{α/2} < z < z_{α/2}\) dan kita simpulkan bahwa \(μ=μ_0\); bila \(z\) jatuh di luar wilayah itu maka kita tolak Ho dan menerima hipotesis alternatifnya bahwa \(μ≠μ_0\). Wilayah kritik biasanya dinyatakan dalam \(z\) dan bukan dalam \(\overline{x}\).
Varians Tidak Diketahui (Variance Unknown)
Prosedur pengujian hipotesis rata-rata populasi untuk kasus \(μ\) dan \(σ\) tidak diketahui serupa dengan penjelasan di atas. Hanya saja, sekarang kita mengganti \(μ\) dengan \(\overline{x}\) dan \(σ\) dengan \(s\), dan sebaran distribusi normal diganti dengan sebaran student-t. Kita nyatakan dalam definisi berikut.
Definisi:
Untuk hipotesis dua arah
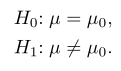
Kita tolak Ho pada tingkat signifikansi \(α\) ketika statistik hitung

lebih besar dari \(t_{α/n,n-1}\) atau kurang dari \(t_{α/n,n-1}\).
Pada Tabel 1 berikut dicantumkan berbagai nilai statistik yang biasa digunakan untuk menguji hipotesis Ho mengenai rata-rata, beserta wilayah kritisnya untuk hipotesis alternatif H1, yang bersifat satu arah atau dua arah.
Tabel 1. Pengujian terkait rata-rata satu populasi

Contoh 1: Dua Arah
Sebuah perusahaan alat olah raga mengembangkan jenis batang pancing sintetik, yang dikatakan mempunyai kekuatan dengan rata-rata 8 kilogram dan simpangan baku 0,5 kilogram. Ujilah hipotesis bahwa \(μ=8\) kilogram lawan alternatifnya \(μ ≠ 8\) kilogram bila suatu sampel acak 50 batang pancing itu setelah dites memberikan kekuatan rata-rata 7,8 kilogram. Gunakan taraf nyata (tingkat signifikansi) sebesar 0,01.
Pembahasan:
Dengan mengikuti langkah-langkah dalam prosedur pengujian hipotesis, kita peroleh
- \(H_0:μ = 8\) kilogram
- \(H_1:μ ≠ 8\) kilogram
- \(α=0,01\).
- Wilayah kritis: \(z < -2,575\) dan \(z > 2,575\), sedangkan dalam hal ini
- Perhitungan: \(\bar{x}= 7,8\) kilogram, \(n = 50\), sehingga
- Keputusan: Tolak Ho dan simpulkan bahwa rata-rata kekuatan batang pancing tidak sama dengan 8.


Contoh 2: Satu Arah
Suatu sampel acak 100 catatan kematian di Amerika Serikat selama tahun lalu menunjukkan umur rata-rata 71,8 tahun, dengan simpangan baku 8,9 tahun. Apakah ini menunjukkan bahwa harapan umur sekarang ini lebih dari 70 tahun? Gunakan taraf nyata 0,05.
Pembahasan:
Dengan mengikuti langkah-langkah dalam prosedur pengujian hipotesis, kita peroleh
- \(H_0:μ = 70\) tahun
- \(H_1:μ > 70\) tahun
- \(α = 0,05\).
- Wilayah kritik: \(z > 1,645\) sedangkan dalam hal ini
- Perhitungan: \(\bar{x}= 71,8\) tahun, \(σ = s = 8,9\) tahun, dan
- Keputusan: Tolak Ho dan simpulkan bahwa harapan umur sekarang ini memang lebih besar daripada 70 tahun


Contoh 3: Satu Arah
Waktu rata-rata yang diperlukan per mahasiswa untuk mendaftarkan diri pada semester ganjil di suatu perguruan tinggi adalah 50 menit dengan simpangan baku 10 menit. Suatu prosedur pendaftaran baru yang menggunakan mesin modern sedang dicoba. Bila suatu sampel acak 12 mahasiswa memerlukan waktu pendaftaran rata-rata 42 menit dengan simpangan baku 11,9 menit dengan menggunakan sistem baru tersebut, ujilah hipotesis bahwa nilai tengah populasinya sekarang kurang dari 50. Gunakan taraf nyata (a) 0,05, dan (b) 0,01. Asumsikan bahwa populasi waktu yang diperlukan adalah normal.
Pembahasan:
Dengan mengikuti langkah-langkah dalam prosedur pengujian hipotesis, kita peroleh
- \(H_0: μ = 50\) menit.
- \(H_1: μ < 50\) menit
- (a) \(α = 0,05\); (b) \(α = 0,01\)
- Wilayah kritik (a) \(t < -1,796\); (b) \(t < -2,718\), sedangkan dalam hal ini
- Perhitungan: \(\bar{x} = 42\) menit, \(s = 11,9\) menit, dan \(n = 12\). Dengan demikian,
- Keputusan: Tolak Ho pada taraf nyata 0,05 tetapi tidak pada taraf nyata 0,01. Pada hakekatnya ini berarti bahwa nilai tengah sebenarnya kemungkinan besar memang lebih kecil daripada 50 menit, tetapi perbedaannya tidak cukup besar untuk mengimbangi biaya yang tinggi untuk mengoperasikan sebuah komputer.

dengan \(v = 11\) derajat bebas.

Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
A wise man learns by the mistakes of others, a fool by his own.
Latin Proverb