
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pendugaan Parameter › Pendugaan Parameter Rata-rata Untuk Satu Populasi
Pendugaan Parameter
Pendugaan Parameter Rata-rata Untuk Satu Populasi
Salah satu penduga titik bagi rata-rata populasi \(μ\) adalah statistik \(\overline{X}\). Distribusi sampling (sampling distribution) dari \(\overline{X}\) berpusat di \(μ\)
Dalam banyak kesempatan, mengestimasi rata-rata populasi bermanfaat dalam penelitian bisnis. Misalnya, manajer sumber daya manusia di sebuah perusahaan ingin memperkirakan rata-rata jumlah hari kerja yang dilewatkan seorang karyawan per tahun karena sakit.
Jika perusahaan memiliki ribuan karyawan, penghitungan langsung rata-rata populasi seperti ini secara praktis tidak mungkin karena besarnya sumber daya yang harus dikeluarkan berupa biaya, tenaga, dan waktu. Sebaliknya, sampel karyawan secara acak dapat diambil, dan rata-rata sampel dari jumlah hari sakit dapat digunakan untuk memperkirakan rata-rata populasi.
Salah satu penduga titik bagi rata-rata populasi \(μ\) adalah statistik \(\overline{X}\). Distribusi penarikan sampel (sampling distribution) \(\overline{X}\) berpusat di \(μ\), dan dalam sebagian besar penerapannya, ragamnya lebih kecil daripada ragam penduga-penduga lainnya. Oleh karena itu, rata-rata sampel \(\overline{x}\) digunakan sebagai nilai dugaan titik bagi rata-rata populasi \(μ\).
Kita tahu bahwa \( \sigma_{\overline{x}}^2 = \displaystyle{ \frac{\sigma^2}{n} } \) sehingga sampel yang besar akan menghasilkan nilai \(\overline{X}\) yang berasal dari suatu distribusi sampling dengan ragam yang kecil. Dengan demikian, bila \(n\) besar maka \(\overline{x}\) akan merupakan nilai dugaan yang sangat akurat bagi \(μ\).
Bila sampel diperoleh dari suatu distribusi normal, atau bila \(n\) cukup besar, kita dapat memperoleh selang kepercayaan bagi \(μ\) dengan mempelajari distribusi sampling bagi \(\overline{X}\). Kita tahu bahwa distribusi sampling bagi \(\overline{X}\) adalah normal dengan rata-rata \(\mu_{\overline{x}} =\mu \) dan simpangan baku \(\sigma_{\overline{x}} = \sigma/\sqrt{n} \).
Dengan melambangkan \(z_{α/2}\) bagi nilai \(z\) yang luas daerah di sebelah kanan di bawah kurva normalnya adalah \(α/2\), kita dapat melihat dari Gambar 1 bahwa

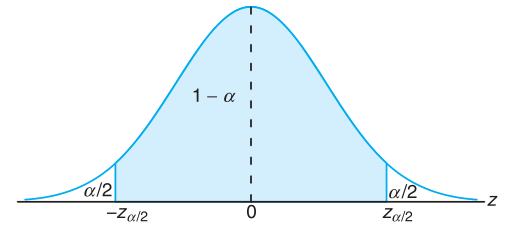
Gambar 1. \( P(-z_{α/2} < Z < z_{α/2}) = 1-α \)
Sedangkan dalam hal ini

Dengan demikian,
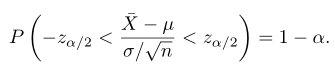
Dengan berturut-turut mengalikan setiap suku ketaksamaan tersebut dengan \(σ/\sqrt{n}\), diikuti dengan mengurangkan \(\overline{X}\) dari setiap suku, dan terakhir mengalikan ketaksamaan tersebut dengan -1, kita peroleh
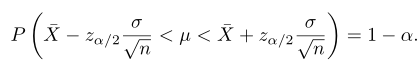
Selang Kepercayaan bagi \(\mu\); \( \ σ\) diketahui
Bila \(\overline{x}\) adalah rataan sampel acak berukuran \(n\) yang diambil dari suatu populasi dengan ragam \(σ^2\) diketahui, maka selang kepercayaan (1-α)100% bagi \(μ\) adalah
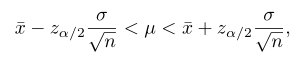
Sedangkan \(z_{α/2}\) adalah nilai \(z\) yang luas daerah di sebelah kanan di bawah kurva normal baku adalah α/2.
Untuk sampel kecil yang diambil dari populasi yang tidak normal, kita tidak dapat mengharapkan bahwa derajat kepercayaan bagi selang tersebut akan akurat. Tetapi bila ukuran sampelnya \(n≥30\), bagaimanapun bentuk populasinya, teori penarikan sampel menjamin akan diperolehnya hasil yang memuaskan.
Untuk menghitung selang kepercayaan \((1-α)100\)% bagi \(μ\), kita telah mengasumsikan bahwa \(σ\) diketahui. Karena asumsi ini biasanya tidak berlaku, kita akan mengganti \(σ\) dengan simpangan baku sampel \(s\), asalkan \(n≥30\).
Contoh 1:
Suatu sampel acak 36 mahasiswa tingkat akhir menghasilkan rata-rata dan simpangan baku nilai matematika berturut-turut adalah 2.6 dan 0.3. Hitunglah selang kepercayaan 95% dan 99% bagi rata-rata nilai matematika seluruh mahasiswa tingkat akhir.
Pembahasan:
Nilai dugaan titik bagi \(μ\) adalah \(\overline{x} =2.6 \). Karena ukuran sampelnya besar, simpangan baku \(σ\) dapat diduga dengan \(s = 0.3\). Dari Tabel Nilai Luas di Bawah Kurva Normal, nilai \(z\) yang luas daerah di sebelah kanannya 0.025, yang berarti pula luas daerah di sebelah kirinya 0.975, adalah \(z_{0.025}=1.96\). Dengan demikian, selang kepercayaan 95% bagi \(μ\) adalah

yang setelah disederhanakan menghasilkan
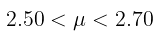
Untuk memperoleh selang kepercayaan 99%, kita harus terlebih dulu menentukan nilai \(z\) yang luas daerah di sebelah kanannya 0.005 dan di sebelah kirinya 0.995. Dengan demikian, sekali lagi dengan menggunakan Tabel Nilai Luas di Bawah Kurva Normal, kita peroleh \(z_{0.005}=2.575\) dan selang kepercayaan 99% bagi \(μ\) adalah

yang setelah disederhanakan menghasilkan selang
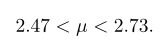
Galat dalam Pendugaan μ
Bila \(\overline{x}\) digunakan untuk menduga \(μ\), kita percaya (1-α)100% bahwa galatnya tidak akan melebihi \( z_{α/2} \, σ/\sqrt{n} \).
Ukuran Sampel bagi Pendugaan \(μ\)
Bila \(\overline{x}\) digunakan untuk menduga \(μ\), kita boleh percaya \((1-α)100\)% bahwa galatnya tidak akan melebihi suatu nilai tertentu \(e\) bila ukuran sampelnya diambil sebesar
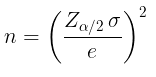
Bila menyelesaikan persamaan itu untuk ukuran sampel \(n\), semua pecahan harus dibulatkan ke bilangan bulat berikutnya yang lebih besar. Dengan selalu mematuhi aturan ini, kita boleh yakin bahwa derajat kepercayaannya tidak pernah jatuh di bawah \((1-α)100\)%.
Contoh 2:
Seberapa besar sampel harus diambil dalam Contoh 1 bila kita ingin percaya 95% bahwa nilai dugaan kita tidak menyimpang dari \(μ\) lebih daripada 0.05?
Simpangan baku sampel s = 0.3 yang diperoleh dari sampel awal berukuran 36 akan digunakan sebagai σ, maka

Jadi, kita percaya 95% bahwa suatu sampel acak berukuran 139 akan menghasilkan nilai dugaan \(\overline{x}\) yang selisihnya dari \(\mu\) tidak akan melebihi 0.05.
Selang Kepercayaan bagi \(μ\) untuk sampel berukuran kecil; \(σ\) Tidak Diketahui.
Bila \(\overline{x}\) dan \(s\) adalah nilai tengah dan simpangan baku sampel berukuran \(n < 30\), yang diambil dari suatu populasi berbentuk genta yang ragamnya \(σ^2\) tidak diketahui, maka selang kepercayaan (1-α)100% bagi \(μ\) diberikan oleh rumus

sedangkan dalam hal ini \(t_{α/2}\) adalah nilai \(t\) dengan \(v = n -1\) derajat bebas yang di sebelah kanannya terdapat daerah seluas \(α/2\).
Contoh 3:
Isi 7 kaleng asam sulfat adalah 9.8, 10.2, 10.4, 9.8, 10.0, 10.2 dan 9.6 liter. Tentukan selang kepercayaan 95% bagi nilai tengah isi semua kaleng demikian ini bila isi kaleng itu menyebar normal.
Pembahasan:
Rata-rata dan simpangan baku data tersebut adalah
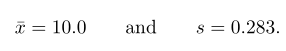
Dengan menggunakan Tabel Nilai Kritis Distribusi-t, kita memperoleh \(t_{0.025}=2.447\) untuk \(v=6\) derajat bebas. Dengan demikian, selang kepercayaan 95% bagi \(μ\) adalah

yang setelah disederhanakan menjadi

Sumber:
Black, Ken. (2010). Business Statistics: For Contemporary Decision Making, 6th ed. Hoboken, NJ: John Wiley & Sons, Inc.
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
Keep your eyes on the stars and your feet on the ground.
Theodore Roosevelt