
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Uji Normalitas › Uji Lilliefors
Normalitas
Uji Lilliefors
Uji Liliefors digunakan untuk memeriksa kenormalan suatu peubah acak dan merupakan alternatif bagi Uji Kolmogorov Smirnov jika rata-rata dan varians populasi tidak diketahui.
Uji Liliefors digunakan untuk memeriksa kenormalan suatu peubah acak sama seperti uji Kolmogorov Smirnov. Ketika rata-rata dan varians populasi diketahui kita menggunakan uji Kolmogorov-Smirnov, akan tetapi jika rata-rata dan varians populasi tidak diketahui, kita menggunakan uji Liliefors.
Uji Liliefors menggunakan pendekatan yang sama dengan Uji Kolmogorov-Smirnov, hanya saja dalam Uji Liliefors kita gunakan tabel nilai kritis Liliefors.
Tahapan Uji Liliefors
Untuk melakukan pengujian normalitas dengan uji kolmogorov-smirnov, kita dapat mengikuti beberapa langkah berikut:
- Tentukan hipotesis
- Tentukan tingkat signifikansi
- Menghitung statistik uji
- Wilayah kritis:
- Keputusan: Tolak Ho pada suatu taraf nyata tertentu jika uji statistik \(L\) melebihi \(α\) yang ditunjukkan pada tabel Liliefors.
- Kesimpulan
Ho: Populasi mengikuti distribusi normal
H1: Populasi tidak mengikuti distribusi normal
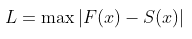
\(L =\) nilai tertinggi dari perbedaan antara \(S(x)\) dan \(F(x)\)
Untuk mendapatkan gambaran yang lebih jelas mengenai uji normalitas Liliefors, perhatikanlah contoh berikut.
Contoh 1:
Sebuah sampel acak berukuran \(n = 6\) dengan nilai pengamatan
| 7 | 9 | 11 | 12 | 14 | 15 |
Tentukanlah apakah populasi sampel tersebut menyebar normal?
Pembahasan:
Dari data tersebut kita peroleh \(\overline{x}=11,3333\) dan \(s = 3,0111\)
- Tentukan hipotesis
- Tingkat signifikansi yang digunakan 0,05 (α=5%)
- Menghitung statistik uji
- Keputusan: Karena \(L < L_{0,05}(6)\) maka tidak tolak Ho
- Kesimpulan: Dengan tingkat signifikansi 5% dapat disimpulkan bahwa populasi mengikuti distribusi normal.
Ho: Populasi mengikuti distribusi normal
H1: Populasi tidak mengikuti distribusi normal
| \( X \) | \( S(X) \) | \( Z \) | \( F(X) \) | \( F(X)-S(X) \) |
|---|---|---|---|---|
| 7 | 0,1667 | -1,44 | 0,0764 | 0,0903 |
| 9 | 0,3333 | -0,77 | 0,2206 | 0,1127 |
| 11 | 0,5000 | -0,11 | 0,4562 | 0,0438 |
| 12 | 0,6667 | 0,22 | 0,5871 | 0,0796 |
| 14 | 0,8333 | 0,89 | 0,8133 | 0,0200 |
| 15 | 1,000 | 1,22 | 0,8888 | 0,1112 |
Kolom keempat F(x) diperoleh dari:

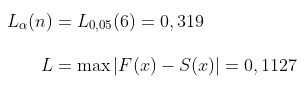
Artikel Terkait
Every block of stone has a statue inside it and it is the task of the sculptor to discover it.
Michelangelo