
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pengujian Hipotesis › Uji Hipotesis Proporsi Dua Populasi
Pengujian Hipotesis
Uji Hipotesis Proporsi Dua Populasi
Sering kali kita berhadapan dengan masalah yang mengharuskan kita menguji hipotesis apakah dua proporsi adalah sama. Misalnya kita ingin menunjukkan bahwa proporsi dokter anak di suatu daerah lebih besar daripada proporsi dokter anak di daerah lain.
Sering kali kita berhadapan dengan masalah yang mengharuskan kita menguji hipotesis apakah dua proporsi adalah sama. Misalnya saja kita ingin menunjukkan bahwa proporsi dokter anak di suatu daerah lebih besar daripada proporsi dokter anak di daerah lain.
Seorang perokok misalnya saja akan memutuskan berhenti merokok hanya bila ia merasa yakin bahwa proporsi perokok yang menderita kanker paru-paru lebih besar daripada proporsi bukan perokok yang menderita kanker paru-paru.
Secara umum, kita ingin menguji hipotesis nol bahwa dua proporsi, atau parameter binomial, adalah sama yakni, kita ingin menguji apakah \(p_1 = p_2\) terhadap salah satu dari alternatifnya \(p_1 < p_2, p_1 > p_2\) atau \(p_1≠p_2\). Tentu saja ini ekivalen dengan menguji hipotesis nol bahwa \(p_1 – p_2 = 0\) lawan alternatifnya \(p_1 – p_2 < 0, p_1 – p_2 > 0\), atau \(p_1-p_2≠0\).
Statistik yang akan dijadikan landasan pengambilan keputusan adalah peubah acak \(\hat{P}_1-\hat{P}_2\). Dua sampel bebas berukuran \(n_1\) dan \(n_2\) diambil secara acak dari dua populasi binomial, dan kemudian proporsi keberhasilan \(\hat{P}_1\) dan \(\hat{P}_2\) dihitung.
Kita tahu bahwa untuk \(n_1\) dan \(n_2\) yang cukup besar, maka pendugaan titik \(\hat{P}_1\) dan \(\hat{P}_2\) akan mendekati distribusi normal dengan rata-rata

dan varian

Oleh karena itu, wilayah kritis bisa dibangun dengan menggunakan peubah normal standar yakni
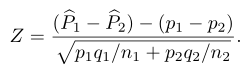
Saat Ho adalah benar, kita dapat substitusi \(p_1 = p_2 = p\) dan \(q_1 = q_2 = q\) ke rumus \(Z\) sehingga

Akan tetapi, untuk menghitung \(Z\), kita harus menduga nilai \(p\) yang berada dalam radikal (di bawah tanda akar). Dengan menggabungkan data dari kedua sampel, diperoleh nilai dugaan gabungan bagi proporsi \(p\) (pooled estimate of the proportion \(p\)), yaitu

di mana \(x_1\) dan \(x_2\) adalah banyaknya keberhasilan dalam masing-masing sampel tersebut. Dengan substitusi \(\hat{p}\) bagi \(p\) dan \(\hat{q}=1-\hat{p}\) bagi \(q\), nilai \(z\) untuk pengujian \(p_1 = p_2\) dengan demikian menjadi

Wilayah kritik bagi hipotesis alternatif ditentukan dengan menggunakan titik kritis bagi kurva normal baku. Oleh karena itu, untuk uji dua-arah dengan taraf nyata \(α\), wilayah kritisnya adalah \(z<-z_{α/2}\) dan \(z>z_{α/2}\). Bila alternatifnya satu-arah \(p_1 < p_2\), wilayah kritiknya adalah \(z<-z_α\), dan bila alternatifnya \(p_1>p_2\), maka wilayah kritisnya \(z>z_α\).
Untuk menguji hipotesis bahwa kedua proporsi itu sama, bila ukuran sampelnya besar, kita dapat menggunakan langkah-langkah berikut ini:
- \(H_0:p_1=p_2\).
- \(H_1\): Alternatifnya adalah \(p_1 < p_2, p_1>p_2\), atau \(p_1≠p_2\).
- Tentukan tingkat signifikansi \(α\).
- Perhitungan: Hitunglah
- Wilayah kritisnya: \(z<-z_α\) bila alternatifnya \(p_1 < p_2, z>z_α\) bila alternatifnya \(p_1>p_2, z<-z_{α/2}\) dan \(z>z_{α/2}\) bila alternatifnya \(p_1≠p_2\).
- Keputusan: Tolak Ho bila \(z\) jatuh ke dalam wilayah kritis; dan terima Ho bila \(z\) jatuh ke dalam wilayah penerimaan.

dan kemudian menghitung

Contoh 1:
Suatu pemungutan suara hendak dilakukan di antara penduduk suatu kota dan sekitarnya untuk mengetahui pendapat mereka mengenai rencana pendirian sebuah gedung pertemuan serba guna. Lokasi gedung yang akan dibangun itu di dalam kota, sehingga para penduduk yang tinggal di sekitar kota itu merasa bahwa rencana itu akan lolos karena besarnya proporsi penduduk kota yang menyetujuinya.
Untuk mengetahui apakah ada selisih yang nyata antara proporsi penduduk kota dan penduduk di sekitar kota itu yang menyetujui rencana tersebut, diambil suatu sampel acak. Bila ternyata 120 di antara 200 penduduk kota dan 240 di antara 500 penduduk di sekitar kota menyetujui rencana tersebut, apakah anda setuju bila dikatakan bahwa proporsi penduduk kota yang menyetujui rencana tersebut lebih tinggi daripada proporsi penduduk di sekitar kota yang menyetujui rencana tersebut? Gunakan taraf nyata 0,025.
Pembahasan:
Misalkan \(p_1\) dan \(p_2\) adalah proporsi sebenarnya penduduk kota dan sekitar kota yang menyetujui rencana tersebut. Sekarang kita ikuti langkah-langkah yang disarankan di atas:
- \(H_0:p_1=p_2\)
- \(H_1:p_1>p_2\).
- \(α=0,025\).
- wilayah kritik: \(z>1,96\)
- Perhitungan:
- Keputusan: Tolak Ho dan kita setuju dengan pendapat bahwa proporsi penduduk kota yang menyetujui rencana itu lebih besar daripada proporsi penduduk sekitar kota yang menyetujui rencana tersebut.

Oleh karena itu,

Contoh 2:
Sebuah perusahaan memproduksi roti rasa keju dan rasa coklat. Bagian marketing mengatakan bahwa penjualan roti rasa keju lebih tinggi dibanding penjualan roti rasa coklat. Hasil survei menunjukkan bahwa 50 di antara 200 konsumen menyukai roti rasa keju dan 20 di antara 200 konsumen menyukai roti rasa coklat. Ujilah pendapat di atas dan carilah selisih persentase penjualan roti tersebut. Gunakan taraf signifikansi 8%.
Pembahasan:
- Rumuskan hipotesis nol dan hipotesis alternatif.
- Taraf signifikansi 8% sehingga \(z_0,04=±1,75\)
- Wilayah kritis penolakan: \(z_0>1,75\)
- Pengujian statistik
- Karena \(z_0=3,95>1,75\), maka hipotesis nol ditolak. Dapat disimpulkan bahwa kita setuju bahwa proporsi penjualan roti rasa keju memang lebih tinggi daripada proporsi penjualan roti rasa coklat dengan taraf signifikansi 8%.
\(H_0:p_1=p_2\)
\(H_1:p_1>p_2\)
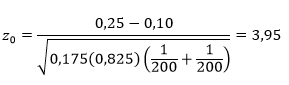
Artikel Terkait
To be successful, you must act big, think big and talk big.
Unknown