Metode Statistika II   »   Pendugaan Parameter   ›  Pendugaan Parameter Proporsi Dua Populasi

Pendugaan Parameter

Pendugaan Parameter Proporsi Dua Populasi

Penduga titik bagi selisih antara dua proporsi populasi \(p_1-p_2\) diberikan oleh statistik \(\hat{P}_1-\hat{P}_2\). Jadi, selisih antara proporsi sampel \(\hat{p}_1-\hat{p}_2\) merupakan nilai dugaan bagi \(p_1-p_2\).

Misalkan kita ingin menduga selisih antara dua parameter binomial \(p_1\) dan \(p_2\). Parameter \(p_1\), misalkan saja, adalah proporsi perokok yang menderita kanker paru-paru, sedangkan \(p_2\) adalah proporsi bukan perokok yang menderita kanker paru-paru. Jadi, masalah kita adalah menduga selisih antara kedua proporsi itu.

Pertama-tama kita mengambil sampel acak berukuran \(n_1\) dari suatu populasi binomial yang mempunyai rata-rata \(n_1p_1\) dan \(n_2p_2\) dan varians \(n_1p_1q_1\) dan \(n_2p_2q_2\). Kemudian hitunglah banyaknya penderita kanker paru-paru dalam masing-masing sampel tersebut, misalkan \(x_1\) dan \(x_2\), serta hitunglah \(\hat{p}_1=x_1/n_1\) dan \(\hat{p}_2=x_2/n_2\).

Penduga titik bagi selisih antara kedua proporsi populasi \(p_1-p_2\) diberikan oleh statistik \(\hat{P}_1-\hat{P}_2\). Dengan demikian, selisih antara proporsi sampel \(\hat{p}_1-\hat{p}_2\) akan digunakan sebagai nilai dugaan bagi \(p_1-p_2\).

Selang kepercayaan bagi \(p_1-p_2\) dapat disusun berdasarkan sebaran penarikan sampel \(\hat{P}_1-\hat{P}_2\). Bila \(n_1\) dan \(n_2\) cukup besar, kita mengetahui bawa \(\hat{P}_1\) dan \(\hat{P}_2\) masing-masing mempunyai sebaran yang menghampiri normal, dengan rata-rata \(p_1\) dan \(p_2\) dan varians \(p_1q_1/n_1\) dan \(p_2q_2/n_2\).

Karena kedua sampel itu bebas satu sama lain, maka peubah acak \(\hat{P}_1\) dan \(\hat{P}_2\) juga bebas, sehingga kita dapat menyimpulkan bahwa \(\hat{P}_1-\hat{P}_2\) kira-kira menyebar normal dengan rata-rata

dan varians

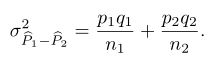
Dengan demikian, kita dapat menyatakan bahwa

Sedangkan dalam hal ini

dan \(z_{α/2}\) adalah nilai peubah acak normal baku yang di sebelah kanannya terdapat daaerah seluas \(α/2\). Dengan mensubstitusikan \(Z\) kita dapat menuliskan pernyataan peluang di atas menjadi

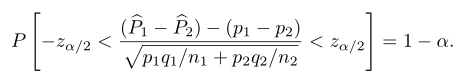
Setelah melakukan manipulasi aljabar seperlunya, kita mengganti \(p_1\) dan \(p_2\) dengan nilai dugaannya masing-masing \(\hat{P}_1=x_1/n_1\) dan \(\hat{p}_2=x_2/n_2\), asalkan \(n_1\) dan \(n_2\) keduanya cukup besar, sehingga diperoleh selang kepercayaan kira-kira \((1-α)100\)% bagi \(p_1-p_2\).

Selang Kepercayaan Sampel Besar bagi \(p_1-p_2\) untuk Sampel Berukuran Besar.

Bila \(\hat{p}_1\) dan \(\hat{p}_2\) masing-masing adalah proporsi keberhasilan dalam sampel acak yang berukuran \(n_1\) dan \(n_2\) serta \(\hat{q}_1 = 1- \hat{p}_1 \) dan \(\hat{q}_2 = 1- \hat{p}_2 \), maka selang kepercayaan kira-kira (1-α)100% bagi selisih antara dua parameter binom \(p_1-p_2\) adalah

sedangkan dalam hal ini \(z_{α/2}\) adalah nilai z yang luas daerah di sebelah kanannya sebesar α/2.

Contoh 1:

Suatu pengumpulan pendapat umum dilakukan terhadap penduduk kota dan penduduk di sekitar kota tersebut untuk menyelidiki kemungkinan diajukannya rencana pembangunan suatu kompleks gedung serba guna. Bila 2400 di antara 5000 penduduk kota dan 1200 di antara 2000 penduduk di sekitar kota tersebut yang diwawancarai menyetujui rencana tersebut, buat selang kepercayaan 90% bagi selisih proporsi sebenarnya yang menyetujui rencana tersebut.

Pembahasan:

Misalkan \(p_1\) dan \(p_2\) masing-masing adalah proporsi sebenarnya penduduk kota dan daerah sekitarnya yang menyetujui rencana tersebut. Maka \(\hat{p}_1=2400/5000=0,48,\) \(\hat{p}_2 =1200/2000=0,60\), dan \(p_1-p_2\) diduga sebesar \(\hat{p}_1-\hat{p}_2 =0,48-0,60=-0,12\).

Dengan menggunakan Tabel Distribusi Normal, kita memperoleh \(z_{0,05}=1,645\). Dengan demikian, selang kepercayaan 90% bagi \(p_1-p_2\) adalah

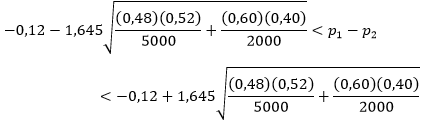
yang setelah disederhanakan menjadi

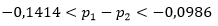
Karena kedua titik ujung selangnya negatif, maka kita juga dapat menyimpulkan bahwa proporsi penduduk sekitar kota yang menyetujui rencana tersebut lebih besar daripada proporsi penduduk kota yang menyetujui rencana tersebut.

Sumber:

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.