
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pendugaan Parameter › Pendugaan Parameter Proporsi Dua Populasi
Pendugaan Parameter
Pendugaan Parameter Proporsi Dua Populasi
Penduga titik bagi proporsi \(p\) dalam suatu percobaan binomial diberikan oleh statistik \(\hat{p}= X/n\), di mana \(X\) menyatakan banyaknya keberhasilan dalam \(n\) percobaan.
Para peneliti dan pengambil keputusan baik itu di pemerintahan maupun swasta sering kali perlu memperkirakan proporsi populasi. Berikut ini adalah beberapa contoh mengapa perlu memperkirakan proporsi populasi:
- Untuk sebagian besar bisnis, memperkirakan pangsa pasar (proporsi pasar mereka) merupakan hal yang penting karena banyak keputusan perusahaan berevolusi dari informasi mengenai pangsa pasar.
- Perusahaan menghabiskan ribuan dolar untuk memperkirakan proporsi barang yang diproduksi dengan kondisi cacat.
- Peluang segmentasi pasar berasal dari pengetahuan tentang proporsi berbagai karakteristik demografi di antara pelanggan atau klien yang potensial.
Penduga titik (estimate point) bagi proporsi populasi \(p\) dalam suatu percobaan binomial diberikan oleh statistik \(\hat{p}= X/n\), di mana \(X\) menyatakan banyaknya keberhasilan dalam \(n\) percobaan. Dengan demikian, proporsi sampel \(\hat{p}=x/n\) akan digunakan sebagai nilai dugaan titik bagi parameter \(p\) tersebut.
Bila proporsi \(p\) yang tidak diketahui itu tidak terlalu dekat pada nol atau 1, kita dapat membuat selang kepercayaan bagi \(p\) dengan mempelajari distribusi sampling bagi \(\hat{P}\).
Menurut Teorema Limit Pusat (Central Limit Theorem), untuk \(n\) yang cukup besar, sebaran bagi \(\hat{P}\) menghampiri normal dengan rata-rata
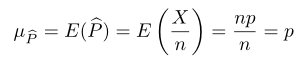
dan varians
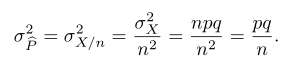
Dengan demikian, kita dapat menyatakan bahwa
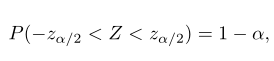
Sedangkan dalam hal ini
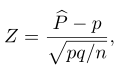
dan \(z_{α/2}\) adalah nilai peubah acak normal baku yang di sebelah kanannya terdapat daerah seluas \(α/2\). Dengan mensubstitusikan \(Z\) kita peroleh

Selang Kepercayaan bagi \(p\) untuk sampel berukuran besar
Bila \(\hat{p}\) adalah proporsi keberhasilkan dalam suatu sampel acak berukuran \(n\), dan \(\hat{q} = 1-\hat{p} \), maka selang kepercayaan kira-kira \((1-α)100\%\) bagi parameter binom \(p\) diberikan oleh
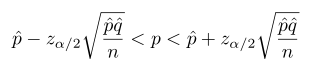
sedangkan \(z_{α/2}\) adalah nilai \(z\) yang luas daerah di sebelah kanannya sebesar \(α/2\).
Contoh 1:
Dari suatu sampel acak 500 orang yang makan siang di sebuah restoran selama beberapa hari Jumat, diperoleh informasi \(x = 160\) orang yang menyukai makanan laut (seafood). Tentukan selang kepercayaan 95% bagi proporsi sesungguhnya orang yang menyukai makanan laut untuk makan siangnya pada hari Jumat di restoran ini.
Pembahasan:
Nilai dugaan titik bagi \(p\) adalah \(\hat{p} = 160/500=0,32\). Dengan menggunakan Tabel Distribusi Normal kita memperoleh \(z_{0,025} = 1,96\). Jadi, dengan mensubstitusikan ke dalam rumus

Kita peroleh selang kepercayaan 95%

yang setelah disederhanakan menghasilkan

Galat dalam Pendugaan \(p\)p
Bila \(\hat{p}\) digunakan sebagai nilai dugaan titik bagi \(p\), maka kita dapat percaya \((1-α)100\%\) bahwa galatnya tidak lebih besar dari \(z_{α/2}\,\sqrt{\hat{p}\hat{q}/n}\).
Ukuran Sampel bagi Pendugaan p
Bila \(\hat{p}\) digunakan untuk menduga \(p\), maka kita percaya (1-α)100% bahwa galatnya tidak melebihi suatu besaran tertentu \(e\) bila ukuran sampelnya diambil sebesar

Contoh 2:
Berapa besar ukuran sampel yang diperlukan dalam Contoh 1 bila kita menginginkan percaya 95% bahwa nilai dugaan bagi \(p\) yang dihasilkan berada dalam 0,02 dari nilai \(p\) yang sebenarnya?
Pembahasan:
Baiklah kita pandang 500 orang tersebut sebagai contoh awal yang memberikan nilai dugaan \(\hat{p} = 0,32\). Dengan demikian,

Jadi, bila kita mendasarkan pada suatu sampel acak 2090 orang, kita boleh percaya 95% bahwa proporsi sampel yang dihasilkannya tidak akan berbeda lebih daripada 0,02 dari proporsi yang sebenarnya.
Ukuran Sampel untuk Pendugaan \(p\)
Bila \(\hat{p}\) digunakan sebagai suatu nilai dugaan bagi \(p\), maka kita percaya sekurang-kurangnya (1-α)100% bahwa galatnya tidak akan melebihi suatu besaran tertentu \(e\) bila ukuran sampelnya

Contoh 3:
Berapa besarnya ukuran sampel yang diperlukan dalam Contoh 1 bila kita ingin percaya sekurang-kurangnya 95% bahwa nilai dugaan bagi \(p\) yang dihasilkannya berada dalam jarak sebesar-besarnya 0,02?
Tidak seperti pada Contoh 2, misalkan kita di sini tidak mempunyai sampel awal yang dapat memberikan sebuah nilai dugaan bagi \(p\). Akibatnya, kita dapat percaya sekurang-kurangnya 95% bahwa nilai proporsi contoh kita tidak akan berselisih lebih daripada 0,02 dengan proporsi populasi sebenarnya bila kita mengambil ukuran sampel sebesar
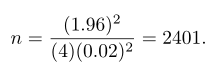
Dengan membandingkan hasil-hasil pada Contoh 2 dan 3, kita melihat bahwa informasi mengenai \(p\), baik yang berasal dari sampel awal ataupun dari pengalaman lalu, memungkinkan kita mengambil sampel yang lebih kecil dengan tetap memelihara derajat ketelitian yang diinginkan.
Sumber:
Black, Ken. (2010). Business Statistics: For Contemporary Decision Making, 6th ed. Hoboken, NJ: John Wiley & Sons, Inc.
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
The bamboo that bends is stronger than the oak that resists.
Japanese Proverb