Metode Statistika II   »   Pendugaan Parameter   ›  Pendugaan Parameter Ragam Untuk Satu Populasi

Pendugaan Parameter

Pendugaan Parameter Ragam Untuk Satu Populasi

Bila suatu sampel berukuran \(n\) ditarik dari sebuah populasi normal dengan varians \(σ^2\), dan kemudian kita hitung varians sampelnya \(S^2\), maka kita peroleh sebuah nilai bagi statistik \(S^2\) yang merupakan nilai dugaan titik bagi \(σ^2\).

Kadang-kadang dalam analisis statistik, peneliti lebih tertarik pada varians populasi daripada rata-rata atau proporsi populasi. Misalnya, variasi antara pembacaan altimeter pesawat (airplane altimeter readings) harus diminimalkan. Tidaklah cukup hanya mengetahui bahwa secara rata-rata merek altimeter tertentu menghasilkan ketinggian yang benar. Jadi, mengukur variasi altimeter sangat penting.

Lalu bagaimana varians populasi itu diestimasi? Bila suatu sampel berukuran \(n\) ditarik dari sebuah populasi normal dengan varians \(σ^2\), dan kemudian kita hitung varians sampelnya \(S^2\), maka kita peroleh sebuah nilai bagi statistik \(S^2\). Varians sampel ini akan digunakan sebagai nilai dugaan titik bagi \(σ^2\). Dengan demikian, statistik \(S^2\) disebut penduga bagi \(σ^2\).

Selang kepercayaan bagi \(σ^2\) dapat diperoleh dengan menggunakan statistik

Statistik \(X^2\) mempunyai sebaran chi-square dengan \(v=n-1\) saat sampel dipilih dari populasi yang berdistribusi normal. Kita bisa tuliskan (lihat Gambar 1)

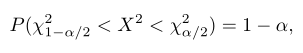
di mana \(χ_{α/2}^2\) dan \(χ_{1-α/2}^2\) adalah nilai-nilai distribusi chi-square dengan \(v = n – 1\) derajat bebas yang luas daerah di sebelah kanannya berturut-turut, adalah \(α/2\) dan \(1-α/2\). Dengan substitusi ke \(X^2\), kita peroleh

Gambar 1. \(P\left( χ_{1-α/2}^2 < X^2 < χ_{α/2}^2 \right) = 1 - α\)

Selang Kepercayaan bagi \(σ^2\).

Bila \(s^2\) adalah varians sampel acak berukuran \(n\) yang ditarik dari suatu populasi normal, maka selang kepercayan (1-α)100% bagi \(σ^2\) diberikan oleh rumus

sedangkan \(χ_{α/2}^2\) dan \(χ_{1-α/2}^2\) adalah nilai-nilai \(χ^2\) dengan \(v = n – 1\) derajat bebas yang luas daerah di sebelah kanannya berturut-turut, adalah \(α/2\) dan \(1-α/2\).

Selang kepercayaan \((1-α)100\)% bagi \(σ\) dapat diperoleh dengan cara mengakarkan kedua ujung selang kepercayaan bagi \(σ^2\).

Contoh 1:

Data berikut ini menyajikan volume 10 kaleng buah persik (dalam desiliter) hasil produksi sebuah perusahaan tertentu:

46.4	46.1	45.8	47.0	46.1
45.9	45.8	46.9	45.2	46.0

Buat selang kepercayaan 95% untuk varians data volume kaleng buah persik hasil perusahaan tersebut, bila diasumsikan data volume kaleng tersebut berdistribusi normal.

Pembahasan:

Pertama-tama kita hitung varians sampel \(s^2\), yakni

Untuk mendapatkan selang kepercayaan 95%, maka kita mengambil \(α=0.05\). Selanjutnya, dengan menggunakan Tabel Nilai Kritis Chi-Square dengan derajat bebas \(v = 9\), kita peroleh \(χ_{0.025}^2=19.023\) dan \(χ_{0.975}^2=2.700\). Dengan mensubstitusikannya ke dalam rumus

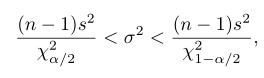
kita memperoleh selang kepercayaan 95% bagi \( σ^2 \), yakni

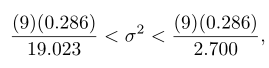
yang setelah disederhanakan menjadi

Dengan demikian, selang kepercayaan 95% untuk varians data volume kaleng buah persik hasil produksi perusahaan tersebut adalah antara 0,135 sampai 0,953.

Sumber:

Black, Ken. (2010). Business Statistics: For Contemporary Decision Making, 6th ed. Hoboken, NJ: John Wiley & Sons, Inc.

Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.