
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE STATISTIKA II
Metode Statistika II
Klasifikasi dalam Statistika
Pendugaan Parameter
Pengujian Hipotesis
Analisis of Varians
Asumsi Normalitas
Asumsi Kesamaan Varians
Metode Statistika II » Pendugaan Parameter › Pendugaan Parameter Ragam Untuk Satu dan Dua Populasi
Pendugaan Parameter
Pendugaan Parameter Ragam Untuk Satu dan Dua Populasi
Nilai dugaan titik untuk rasio dua varians populasi \(σ_1^2/σ_2^2\) diperoleh dari rasio varians sampelnya yakni \(s_1^2/s_2^2\). Jadi, statistik \(S_1^2/S_2^2\) merupakan penduga bagi \(σ_1^2/σ_2^2\).
Oleh Tju Ji Long · Statistisi
Nilai dugaan titik untuk rasio dua varians populasi \(σ_1^2/σ_2^2\) diperoleh dari rasio varians sampelnya yakni \(s_1^2/s_2^2\). Jadi, statistik \(S_1^2/S_2^2\) merupakan penduga bagi \(σ_1^2/σ_2^2\).
Bila \(σ_1^2\) dan \(σ_2^2\) keduanya merupakan varians populasi normal, maka kita dapat membuat selang kepercayaan bagi \(σ_1^2/σ_2^2\) dengan menggunakan statistik

Peubah acak \(F\) mempunyai distribusi \(F\) dengan \(v_1 = n_1 – 1\) dan \(v_2 = n_2 – 1\) derajat bebas. Oleh karena itu, kita bisa tuliskan (lihat Gambar 1)

di mana \(f_{1-α/2} (v_1,v_2 )\) dan \(f_{α/2} (v_2,v_1)\) adalah nilai-nilai sebaran \(F\) dengan \(v_1\) dan \(v_2\) derajat bebas, yang masing-masing di sebelah kanannya terdapat daerah seluas \(1-α/2\) dan \(α/2\).
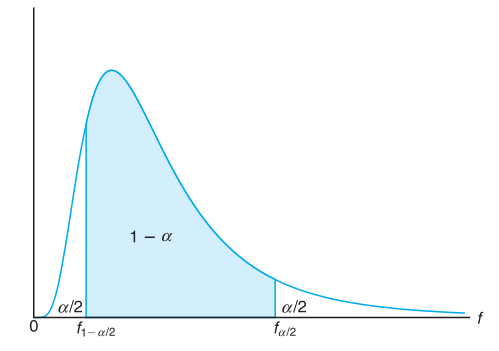
Gambar 1. \( P\left[ f_{1-α/2} (v_1,v_2 ) < F < f_{α/2} (v_1,v_2 ) \right] = 1 - α \)
Dengan mensubstitusikan \(F\) kita peroleh
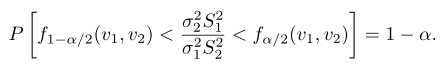
Dengan mengalikan setiap suku dalam ketaksamaan tersebut dengan \(S_2^2/S_1^2\), dan kemudian membalikkan suku-sukunya, kita peroleh
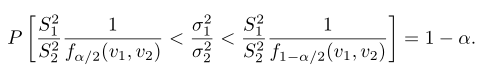
Selanjutnya, kita mengganti \(f_{1-α/2} (v_1,v_2 )\) dengan \(1/f_{α/2} (v_2,v_1 )\), sehingga
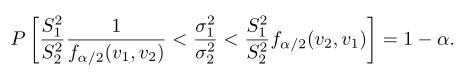
Kita nyatakan hasil yang kita peroleh di atas dalam definisi berikut.
Selang Kepercayaan bagi \(σ_1^2/σ_2^2\)
Bila \(s_1^2\) dan \(s_2^2\) adalah varians dua sampel acak bebas berukuran \(n_1\) dan \(n_2\) yang diambil dari populasi normal, maka selang kepercayaan \((1-α)100\)% bagi \(σ_1^2/σ_2^2\) diberikan oleh

sedangkan dalam hal ini \(f_{α/2}(v_1,v_2 )\) merupakan nilai \(f\) untuk \(v_1 = n_1 – 1\) dan \(v_2 = n_2 – 1\) derajat bebas yang di sebelah kanannya terdapat daerah seluas \(α/2\); dan \(f_{α/2}(v_1,v_2 )\) merupakan nilai \(f\) yang serupa tetapi untuk \(v_2 = n_2 – 1\) dan \(v_1 = n_1 – 1\).
Teorema 1:
Dengan menuliskan \(f_α (v_1,v_2)\) untuk \(f_α\) dengan \(v_1\) dan \(v_2\) derajat bebas, maka

Jadi, nilai \(f\) dengan 6 dan 10 derajat bebas yang di sebelah kanannya terdapat daerah seluas 0,95 adalah

Contoh 1:
Suatu tes penempatan untuk matematika diberikan pada 25 siswa laki-laki dan 16 siswa perempuan. Siswa laki-laki mencapai nilai rata-rata 82 dengan simpangan baku 8, sedangkan siswa perempuan mencapai nilai rata-rata 78 dengan simpangan 7.
Buat selang kepercayaan 98% bagi \(σ_1^2/σ_2^2\) dan \(σ_1/σ_2\), bila \(σ_1^2\) dan \(σ_2^2\) masing-masing adalah varians populasi semua nilai siswa laki-laki dan perempuan yang mungkin mengambil tes tersebut. Asumsikan bahwa populasinya menyebar normal.
Pembahasan:
Dalam hal ini kita mempunyai \(n_1 = 25, n_2 = 16, s_1 = 8\), dan \(s_2 = 7\). Untuk selang kepercayaan 98%, kita harus mengambil \(α=0,02\). Dengan menggunakan Tabel Nilai Kritis F, kita memperoleh \(f_{0,01} (24,15)=3,29\) dan \(f_{0,01} (15,24)=2,89\). Dengan mensubstitusikan nilai-nilai itu ke dalam rumus

kita mendapatkan selang kepercayaan 98% yang dicari, yaitu
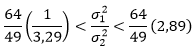
yang setelah disederhanakan menjadi
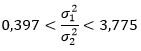
Dengan mengambil akar kedua ujung selang tersebut, kita peroleh selang kepercayaan 98% bagi \(σ_1/σ_2\), yaitu

Sumber:
Walpole, R.E., et al. (2012). Probability & Statistics for Engineers & Scientists, 9th ed. Boston: Pearson Education, Inc.
Artikel Terkait
It is better to be hated for what you are than to be loved for what you are not.
Andre Gide