Metode Statistika I   »   Ukuran Penyebaran Data   ›  Ragam dan Standar Deviasi Data Berkelompok dan Tidak Berkelompok

Ragam dan Standar Deviasi

Ragam dan Standar Deviasi Data Berkelompok dan Tidak Berkelompok

Standar deviasi adalah ukuran yang menunjukkan simpangan nilai pengamatan terhadap rata-ratanya. Nilai standar deviasi yang dikuadratkan disebut ragam atau varians.

Sebagaimana telah kita ketahui bahwa terdapat beberapa ukuran variasi atau penyebaran data yang umum digunakan yakni range, standar deviasi, dan varians. Kita telah membahas tentang range atau jangkauan yang merupakan selisih antara dua nilai yang paling ekstrim (maksimum dan minimum).

Pada artikel ini, kita lanjutkan pembahasan mengenai ukuran penyebaran data yang lainnya yakni standar deviasi dan varians.

Standar deviasi atau dikenal juga dengan simpangan baku merupakan ukuran yang paling sering dijumpai dalam pengukuran variasi data. Ukuran ini menunjukkan simpangan nilai pengamatan terhadap rata-ratanya. Adapun nilai standar deviasi yang dikuadratkan disebut ragam atau varians.

Menghitung Standar Deviasi dan Varians

Penghitungan standar deviasi dan varians dapat dibedakan untuk data populasi dan sampel. Standar deviasi untuk data populasi disimbolkan dengan lambang \(σ\) (dibaca: sigma) dan untuk sampel dinyatakan dengan huruf \(s\) kecil.

Adapun rumus penghitungan standar deviasi untuk data populasi dapat dinyatakan sebagai berikut:

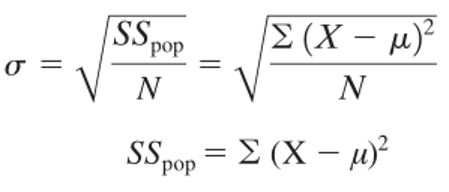
Rumus penghitungan standar deviasi dan varians untuk data sampel tidak jauh berbeda dengan yang telah ditunjukan untuk data populasi. Hanya saja kita mengganti penyebut \(N\) dengan \(N-1\). Penggunaan \(N-1\) ini dilandasi bahwa ketika kita menghitung standar deviasi dari data sampel, kita biasanya menggunakan hasil penghitungan kita untuk mengestimasi standar deviasi populasi dan membagi dengan \(N-1\), alih-alih \(N\), memberikan estimasi yang lebih akurat bagi \(σ\).

Dengan demikian, rumus penghitungan standar deviasi untuk data sampel dapat dinyatakan sebagai berikut:

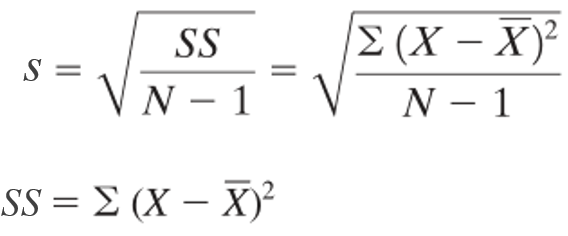
Supaya lebih jelas, perhatikan beberapa contoh soal berikut:

Contoh Soal 1: Data Populasi

Misalkan diketahui variabel \(X\) dengan nilai-nilainya yaitu: 3, 4, 5, 6, dan 7. Hitunglah standar deviasi dan varians dari variabel \(X\) tersebut! (Anggaplah \(X\) sebagai variabel populasi)

Pembahasan:

Contoh Soal 2: Data Sampel

Misalkan diketahui variabel \(X\) dengan nilai-nilainya yaitu: 2, 4, 6, 8, dan 10. Hitunglah standar deviasi dan varians dari variabel \(X\) tersebut! (Anggaplah \(X\) sebagai variabel sampel)

Pembahasan:

Sumber:

Pagano, Robert R. (2013). Understanding Statistics in the Behavioral Sciences, 10th ed. Belmont, CA: Wadsworth/Cengage Learning.