Metode Statistika I   »   Kemencengan dan Keruncingan Data   ›  Arti dan Kegunaan Mengetahui Kemencengan Data

Kemencengan Data

Arti dan Kegunaan Mengetahui Kemencengan Data

Terdapat dua ukuran yang biasa digunakan untuk menjelaskan bentuk distribusi data yakni ukuran kemencengan (skewness) dan ukuran keruncingan (kurtosis).

Ukuran bentuk (measures of shape) bisa digunakan untuk menjelaskan bentuk distribusi data. Terdapat dua ukuran bentuk yaitu ukuran kemencengan (skewness) dan ukuran keruncingan (kurtosis).

Pada bagian ini, kita fokus pada ukuran kemencengan, sedangkan untuk ukuran keruncingan akan dibahas pada artikel lain.

Pengertian kemencengan

Kemencengan atau skewness adalah ketidaksimetrisan (asymmetry) suatu distribusi atau kurva dari bentuknya yang simetris. Distribusi atau kurva yang simetris seperti tergambar pada Gambar 1 di bawah ini mempunyai nilai rata-rata hitung, median, dan modus yang sama besar.

Gambar 1. Distribusi Simetris (Rata-rata hitung = median = modus)

Jika suatu distribusi atau kurva mempunyai ekor yang lebih panjang di bagian kiri (dilihat dari pandangan kita), maka distribusi atau kurva tersebut disebut menjulur ke kiri (skewed to the left) atau mempunyai kemencengan yang negatif (negative skewness). Pada distribusi ini rata-rata hitung lebih kecil dari Median dan Median lebih kecil dari Modus. Untuk distribusi yang menceng kiri atau menceng negatif, data cenderung mengelompok pada sebelah kanan distribusi (Perhatikan Gambar 2a).

Gambar 2. (a) Kurva menceng negatif dan (b) kurva menceng positif

Sebaliknya, jika distribusi mempunyai ekor yang lebih panjang ke kanan (lihat Gambar 2b), maka distribusi tersebut disebut menjulur ke kanan (skewed to the right) atau mempunyai kemencengan yang positif (positive skewness). Pada distribusi ini rata-rata hitung lebih besar dari median dan median lebih besar dari modus. Untuk distribusi yang menceng kanan, data cenderung mengelompok pada sebelah kiri distribusi.

Perhatikan bahwa kemencengan suatu data pada penjelasan di atas dapat dengan mudah diketahui karena data telah disajikan dalam bentuk kurva yang memungkinkan kita untuk menyimpulkan dengan cepat karena bentuknya yang kontras. Namun, bagaimana kita bisa mengetahui kemencengan dari data yang masih mentah atau belum disajikan dalam kurva seperti yang sudah diberikan? Apakah kita harus selalu membuat kurva untuk mengetahui kemencengan?

Tentu saja, kita tidak harus selalu membuat kurva karena itu bukan pekerjaan yang praktis. Selain itu, penilaian kemencengan dengan melihat langsung dari kurva bersifat subjektif. Dengan kata lain, penilaian bisa berbeda antara orang yang satu dengan orang yang lainnya. Misalnya, yang satu menyatakan menceng kiri tetapi yang lain justru menyatakan simetris atau sebaliknya.

Oleh karena itu, di sini kita akan menjelaskan beberapa ukuran yang digunakan untuk menentukan kemencengan suatu data. Dengan ukuran ini, penilaian secara subjektif dapat dihindari.

Beberapa Ukuran Kemencengan

Terdapat beberapa ukuran kemencengan yang umum digunakan, yang mana pada umumnya didasarkan pada seberapa jauh rata-rata hitung berbeda dari modus, atau seberapa jauh rata-rata hitung berbeda dari median.

Semakin jauh rata-rata hitung berbeda dari modus, atau berbeda dari median, maka semakin menceng distribusi tersebut. Selain berdasarkan rata-rata hitung, median, dan modus, kita juga dapat mengetahui kemencengan suatu distribusi atau kurva berdasarkan informasi kuartil.

Beberapa ukuran kemencengan yang biasa dipakai adalah sebagai berikut:

1. Ukuran kemencengan Pearson tipe 1 dan tipe 2;
2. Ukuran kemencengan kuartil (Koefisien kemencengan Bowley);
3. Koefisien kemencengan Kelly;
4. Koefisien kemencengan kurva dengan Moment \((α_3)\).

Kegunaan Ukuran Kemencengan

Pengetahuan tentang kemencengan berguna untuk menggambarkan bentuk suatu distribusi atau kurva dan juga sebagai dasar untuk memilih ukuran pemusatan data (measures of central tendencey) yang mana yang lebih sesuai atau dapat mewakili suatu kelompok data.

Sebagai contoh, bila diketahui kemencengan dari suatu distribusi (katakanlah distribusi pendapatan dari suatu kelompok penduduk) adalah +1.5, maka distribusi tersebut adalah menjulur ke kanan atau menceng positif, yang berarti data cenderung mengelompok pada nilai-nilai yang rendah. Dalam contoh ini, sebagian besar penduduk mempunyai pendapatan yang rendah, dan hanya sebagian kecil yang berpendapatan tinggi.

Seperti dijelaskan di atas, ukuran kemencengan dapat juga digunakan untuk memilih ukuran pemusatan data yang lebih tepat untuk mewakili suatu kelompok data. Sebagai contoh, bila diketahui distribusi data sangat tidak simetris, baik menjulur ke kiri atau pun menjulur ke kanan, maka rata-rata hitung cenderung kurang mewakili kelompok data tersebut, karena rata-rata hitung terpengaruh oleh nilai-nilai pencilan (extreme values atau outliers).

Dalam hal ini, ukuran pemusatan data yang lebih baik digunakan adalah median. Dengan demikian, berdasarkan besaran ukuran skewness yang amat jauh dari 0 (nol), maka dapat ditentukan bahwa rata-rata hitung bukanlah ukuran ‘pusat’ yang disarankan atau yang baik untuk digunakan.

Di samping itu, dalam hal-hal tertentu, ukuran skewness bisa memberikan indikasi perubahan bentuk distribusi suatu variabel antar waktu atau perbedaan bentuk distribusi suatu variabel antar tempat dalam suatu waktu. Perubahan ini bisa bermanfaat dalam membuat suatu kesimpulan atau analisis yang bermanfaat.

Misal, terdapat informasi mengenai rata-rata upah buruh dari dua waktu yang berbeda seperti disajikan dalam Gambar 3. Pada waktu I, distribusi upah buruh adalah menceng kiri. Sedangkan, pada waktu II, distribusi upah telah berubah menjadi menceng kanan. Dengan kata lain, telah terjadi perubahan upah dari yang berdistribusi menceng kiri menjadi menceng kanan.

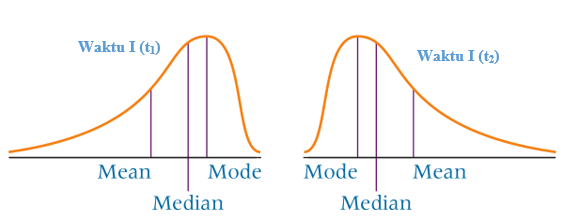
Gambar 3.

Perubahan ini menunjukkan bahwa telah terjadi kenaikan upah (rata-rata hitung pendapatan buruh di waktu II telah lebih besar daripada di waktu I) yang mana merupakan sesuatu yang menggembirakan bagi para kaum buruh.

Akan tetapi, terjadinya perubahan bentuk distribusi tersebut juga memberikan gambaran bahwa jumlah buruh yang memperoleh upah di bawah rata-rata telah bertambah banyak yang mana bukan sesuatu yang menggembirakan karena yang merasa kurang puas juga semakin banyak.

Selain itu, terlihat di waktu II (t2) bahwa banyaknya buruh yang berpendapatan di bawah rata-rata hitung menjadi lebih dari 50% (karena rata-rata hitung lebih besar dari median), sedangkan di waktu I (t1) karena rata-rata hitung lebih kecil dari median, maka banyaknya buruh yang berpendapatan lebih kecil dari rata-rata hitung adalah kurang dari 50%.

Karena, rata-rata hitung biasanya digunakan sebagai patokan rata-rata pendapatan buruh pada umumnya, maka secara relatif semakin banyak buruh yang berpendapatan di bawah rata-rata hitung, yang dapat diartikan secara relatif bahwa semakin banyak buruh yang kurang menikmati kenaikan rata-rata hitung dalam periode tersebut.

Lantas, bagaimana perubahan suatu distribusi, misal distribusi pendapatan atau upah, yang ideal dari waktu ke waktu? Gambar 4 di bawah ini memberikan bentuk perubahan yang ideal dari suatu distribusi pendapatan atau upah, yaitu secara rata-rata (pendapatan atau upah) mengalami kenaikan, dan pada waktu yang bersamaan kemencengan distribusi pendapatan menunjukkan bahwa penduduk atau pekerja telah mengelompok pada tingkat pendapatan atau upah yang tinggi (berbeda dengan pada waktu I dengan pengelompokan penduduk atau pekerja adalah pada tingkat pendapatan yang rendah).

Pada waktu II, persentase penduduk yang mendapat pendapatan atau upah lebih kecil dari rata-rata hitung adalah kurang dari 50% (karena rata-rata hitung < median), sedangkan pada waktu I, persentase penduduk yang memiki upah lebih kecil dari rata-rata hitung adalah lebih dari 50% (karena rata-rata hitung > median).

Gambar 4. Pergeseran kurva dari menceng positif ke menceng negatif.