Metode Statistika I   »   Hubungan Dua Variabel   ›  Koefisien Korelasi Pearson

Korelasi Pearson

Koefisien Korelasi Pearson

Korelasi adalah hubungan antara dua variabel, terutama untuk variabel kuantitatif. Dengan kata lain, ukuran korelasi menggambarkan tingkat hubungan antara dua variabel.

Oleh Tju Ji Long · Statistisi

Korelasi (correlation) adalah hubungan (relationship) antara dua variabel, terutama untuk variabel kuantitatif. Dengan kata lain, ukuran korelasi menggambarkan tingkat hubungan (degree of relationship) antara dua variabel.

Secara statistik, korelasi yang tinggi antara dua variabel hanya menunjukkan kovariasi atau keragaman bersama (baik searah ataupun berlawanan arah) yang erat antara kedua variabel tersebut.

Keragaman bersama ini hanyalah merupakan salah satu syarat (atau indikasi) untuk menarik kesimpulan tentang kemungkinan adanya hubungan kausal antara dua variabel.

Sering kali kita menjumpai istilah asosiasi yang juga menunjukkan hubungan antara dua variabel atau lebih. Lalu, apakah korelasi sama dengan asosiasi (association)? Meskipun korelasi dan asosiasi sama-sama berarti hubungan atau kaitan antara dua atau lebih variabel, tetapi kedua istilah tersebut digunakan secara berbede.

Korelasi adalah ukuran hubungan antara dua variabel kuantitatif atau variabel numerik, sedangkan asosiasi adalah ukuran hubungan antara dua variabel kualitatif atau variabel kategori.

Ukuran yang biasa digunakan untuk mengukur keeratan/kuatnya hubungan antara dua variabel berskala interval adalah koefisien korelasi Pearson, yang sering dinotasikan dengan simbol \(r\) (untuk pengamatan sampel) atau \(ρ\) (untuk parameter, yaitu untuk nilai pada populasi). Perlu diingat bahwa ukuran ini hanya mengukur keeratan hubungan linear (garis lurus) antara 2 (dua) variabel.

Dengan demikian, bisa saja ukuran korelasi ini menunjukkan tidak adanya hubungan (dalam hal ini \(r\) = 0), tetapi kedua variabel tersebut berhubungan erat secara bukan linear, misalnya berkaitan secara parabolik. Kenaikan X akan diikuti oleh kenaikan Y, tetapi setelah pada suatu tingkat nilai X tertentu, kenaikan nilai X akan diikuti dengan penurunan nilai Y.

Rumus yang dapat digunakan untuk menghitung koefisien korelasi Pearson (r) adalah sebagia berikut:

(1)

Nilai \(r\) terletak antara – 1 sampai 1 \((-1≤r≤1)\).

Jika \(r = -1\) berarti antara variabel X dan Y terdapat hubungan linier (garis lurus) yang negatif (berlawanan arah , jika nilai variabel X bertambah besar maka nilai variabel Y akan bertambah kecil, dan sebaliknya jika nilai variabel X bertambah kecil maka nilai variabel Y akan bertambah besar) dan sempurna (semua pasangan nilai X, Y berada pada suatu garis lurus).

Jika \(r = 0\) berarti tidak ada hubungan garis lurus antara variabel X dan Y. Akan tetapi, mungkin saja antara X dan Y terdapat hubungan yang berbentuk bukan garis lurus, misalnya hubungan kuadratik.

Jika \(r = +1\) berarti antara variabel X dan variabel Y terdapat hubungan linier (garis lurus) yang positif (searah, yaitu jika nilai variabel X bertambah besar maka nilai variabel Y akan bertambah besar, dan demikian juga jika nilai variabel X bertambah kecil maka nilai variabel Y akan bertambah kecil) dan sempurna (semua pasangan nilai X, Y berada pada garis lurus).

Terdapat kriteria yang dapat digunakan dalam menentukan derajat kuat tidaknya hubungan antara dua variabel berdasarkan koefisien korelasi Pearson. Kriteria berikut (menggunakan nilai mutlak dari r) dapat digunakan sebagai aturan sederhana (rule of thumb) untuk menentukan derajat kuat tidaknya hubungan antara dua variabel:

\(0<|r|<0,49\) hubungan lemah

\(0,50<|r|<0,79\) hubungan sedang

\(0,80<|r|<1\) hubungan kuat

Contoh 1:

Berdasarkan data berikut (diperoleh dari pasangan data X dan Y), hitunglah koefisien korelasi antara X dan Y!

Pembahasan

Berdasarkan data di atas, koefisien korelasi dari ke dua variabel tersebut adalah:

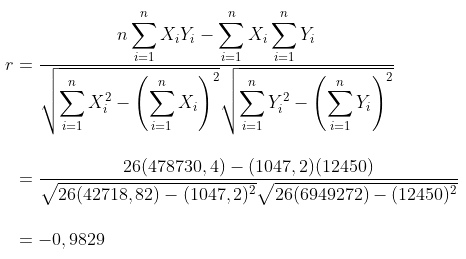
Koefisien korelasi yang diperoleh menunjukkan bahwa ada hubungan negatif (berlawanan arah) yang kuat antara variabel X dengan variabel Y.

Contoh 2:

Ingin diketahui seberapa kuat hubungan (garis lurus) antara besarnya pendapatan dengan pengeluaran konsumsi per bulan. Berdasarkan 6 orang yang diwawancarai, diperoleh data sebagai berikut (data dalam satuan ribuan):

X (pendapatan)	800	900	700	600	700	800
Y (konsumsi)	300	300	200	100	200	200

Pembahasan:

Untuk menghitung koefisien korelasi maka disusun tabel bantu sebagai berikut:

Tabel 1. Tabel bantu penghitungan koefisien korelasi Pearson

Berdasarkan tabel bantu tersebut diperoleh nilai-nilai:

Untuk menghitung koefisien korelasi, maka nilai-nilai tersebut dimasukkan dalam rumus koefisien korelasi sehingga diperoleh sebagai berikut:

Jadi, diperoleh nilai koefisien korelasi (\(r\)) sebesar 0,887. Karena \(r\) bernilai positif dan mendekati 1 berarti hubungan antara konsumsi dan pendapatan adalah kuat dan searah (positif). Dengan kata lain, peningkatan pendapatan seseorang akan diikuti dengan peningkatan pengeluaran (konsumsi).