Tutorial R   »   Statistik Nonparametrik   ›  Uji Run dalam Pemrograman R

Uji Run

Uji Run dalam Pemrograman R

Salah satu uji untuk mengetahui keacakan suatu data yaitu uji run. Untuk melakukan Uji Run pada R, kita dapat menggunakan perintah atau fungsi run.test() yang terdapat pada package tseries.

Keacakan (randomness) data sampel merupakan syarat yang perlu dipenuhi dalam pengambilan sampel dari suatu populasi. Salah satu uji untuk mengetahui keacakan suatu data yaitu uji run yang merupakan uji dalam statistik nonparametrik.

Uji run digunakan untuk mengetahui apakah sederetan data yang terdiri dari dua kategori tersusun secara acak atau tidak.

Untuk melakukan uji run pada R, kita dapat menggunakan fungsi run.test() yang terdapat pada package tseries. Jadi, pastikan package tersebut telah terinstal dalam R.

runs.test(x, exact = FALSE, alternative = c("two.sided", "less", "greater"))
              

Argumen:

Contoh Soal 1:

Seorang peneliti ingin mengetahui apakah pengaturan antrian pria dan wanita di depan tempat pembelian tiket teater mengikuti pengaturan acak. Data diperoleh dengan mencatat jenis kelamin dari urutan 50 orang yang menuju tempat pembelian tiket. Urutan dari 30 pria (P) dan 20 wanita (W) adalah sebagai berikut:

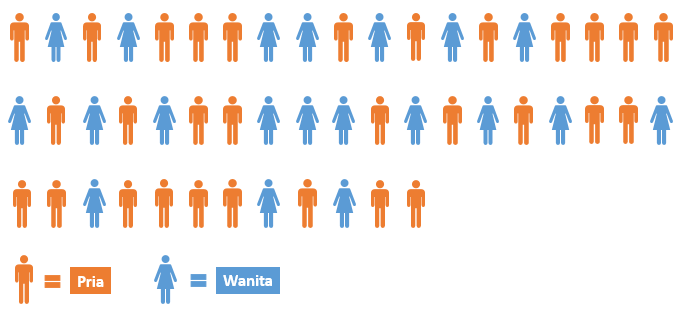
Pembahasan:

Untuk menyelesaikan soal ini, tentu kita harus mengetahui hipotesis nol dan hipotesis alternatifnya terlebih dahulu yakni H₀ : Urutan pria dan wanita dalam antrian adalah acak. H₁ : Urutan pria dan wanita dalam antrian tidak acak. Selanjutnya, tingkat signifikansi yang digunakan yaitu: \(α = 0,05 \).

Sintaks R:

Pertama, install package tseries terlebih dahulu.

                
                  # install.packages("tseries")
                  library(tseries)
                
              

Misalkan kita memberikan kode "1" untuk perempuan dan kode "0" untuk laki-laki, maka kita peroleh berikut ini.

                
                  run <- factor(c(0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 
                                1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 
                                0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 
                                1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 
                                1, 0, 0, 0, 0, 1, 0, 1, 0, 0))
                                
                  runs.test(run, alternative = "two.sided")
                  
                  Output:

                    Runs Test

                  data:  run
                  Standard Normal = 2.9794, p-value = 0.002888
                  alternative hypothesis: two.sided
                
              

Dari output yang dihasilkan di atas, diperoleh nilai p-value untuk uji run yaitu 0.00288. Nilai p-value ini lebih kecil dari tingkat signifikansi uji 0.05. Dengan demikian, kita putuskan tolak Ho dan dapat disimpulkan bahwa dengan tingkat keyakinan 95% kita percaya bahwa urutan antrian tersebut adalah tidak acak.