Tutorial R   »   Statistik Nonparametrik   ›  Uji Friedman dalam Pemrograman R

Uji Friedman

Uji Friedman dalam Pemrograman R

Uji Friedman merupakan uji statistik nonparametrik untuk \(k\) sampel berhubungan. Untuk melakukan uji Friedman dalam R, kita dapat menggunakan perintah friedman_test().

Uji Friedman merupakan uji statistik nonparametrik untuk \(k\) sampel berhubungan. Uji ini digunakan sebagai alternatif ketika ANOVA dua arah dalam statistik parametrik tidak dapat dipakai karena tidak terpenuhinya asumsi yang diharuskan.

Untuk melakukan uji Friedman dalam R, kita dapat menggunakan perintah friedman_test(). Sebagai contoh, kita akan gunakan data selfesteem pada package datarium.

					
					    # menampilkan 3 pengamatan pertama 
						data("selfesteem", package = "datarium")
						head(selfesteem, 3)
						
						Output:
						# A tibble: 3 x 4
						 id    t1    t2    t3
						(int) (dbl) (dbl) (dbl)
						  1   4.01  5.18  7.11
						  2   2.56  6.91  6.31
						  3   3.24  4.44  9.78
					
				

					
					    # mengubah tampilan data menjadi format memanjang ke bawah
						library(dplyr)
						selfesteem <- selfesteem %>%
							gather(key = "time", value = "score", t1, t2, t3) %>%
							convert_as_factor(id, time)
						head(selfesteem, 3)
						
						Output:
						# A tibble: 3 x 3
						  id    time  score
						(fct) (fct) (dbl)
						  1     t1     4.01
						  2     t1     2.56
						  3     t1     3.24
					
				

                  
                    # menampilkan ringkasan statistik (min, max, ...)
                    selfesteem %>%
                      group_by(time) %>%
                      get_summary_stats(score, type = "common")
                      
                    Output:
                      # A tibble: 3 x 11
                    time  variable     n   min   max median   iqr  mean    sd    se    ci
                    (fct) (chr)    (dbl) (dbl) (dbl)  (dbl) (dbl) (dbl) (dbl) (dbl) (dbl)
                    1 t1    score       10  2.05  4.00   3.21 0.571  3.14 0.552 0.174 0.395
                    2 t2    score       10  3.91  6.91   4.60 0.89   4.93 0.863 0.273 0.617
                    3 t3    score       10  6.31  9.78   7.46 1.74   7.64 1.14  0.361 0.817
                  
                

                  
                    # visualisasi data dalam bentuk boxplot
        			ggboxplot(selfesteem, x = "time", y = "score", add = "jitter")
                  
                

Output:

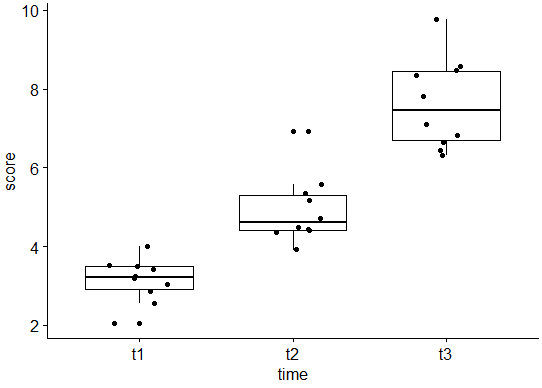
Dari boxplot di atas tampak dengan jelas bahwa ada perbedaan skor yang cukup signifikan untuk ketiga variabel t1, t2, dan t3. Namun, pendapat ini masih bersifat subjektif. Maka itu, dilakukan uji friedman untuk mendapatkan jawaban yang lebih baik.

                  
                    # melakukan uji friedman
					friedman_test(selfesteem,score ~ time |id)
					
					Output:
					# A tibble: 1 x 6
					.y.       n statistic    df        p method       
					* (chr) (int)     (dbl) (dbl)    (dbl) (chr)        
					1 score    10      18.2     2 0.000112 Friedman test
                  
                

Dari output pengujian Friedman di atas diperoleh nilai p-value sebesar 0.00011. Nilai ini lebih kecil dari tingkat signifikan 0.05 maupun 0.01 sehingga keputusan yang diambil adalah gagal tolak Ho dan disimpulkan bahwa terdapat setidaknya dua dari ketiga variabel (t1, t2, t3) tersebut yang berbeda.

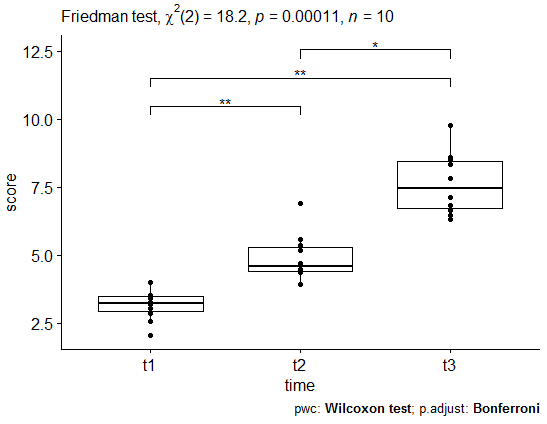
Untuk mengetahui mana saja variabel yang berbeda, maka dilanjutkan dengan melakukan pairwase comparison dengan metode Bonferroni yang mana diperoleh hasil bahwa ketiga variabel tersebut adalah berbeda satu sama lainnya.

                    
						# pairwise comparisons
						pwc <- selfesteem %>% wilcox_test(score ~ time, 
						       paired = TRUE, p.adjust.method = "bonferroni")
						pwc
						
						Output:
						# A tibble: 3 x 9
						.y.   group1 group2    n1    n2 statistic     p p.adj p.adj.signif
						* (chr) (chr)  (chr)  (int) (int)     (dbl) (dbl) (dbl) (chr)       
						1 score t1     t2        10    10         0 0.002 0.006 **          
						2 score t1     t3        10    10         0 0.002 0.006 **          
						3 score t2     t3        10    10         1 0.004 0.012 * 
                    
                

                    
						# Visualization: box plots with p-values
						pwc <- pwc %>% add_xy_position(x = "time")
						ggboxplot(selfesteem, x = "time", y = "score", add = "point") +
							stat_pvalue_manual(pwc, hide.ns = TRUE) +
							labs(
								subtitle = get_test_label(res.fried,  detailed = TRUE),
								caption = get_pwc_label(pwc)
							)
                    
                

Output: