www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
Tutorial R
Tutorial R
Tutorial R » Analisis Regresi › Regresi Linear Sederhana dalam Pemrograman R
Simple Regression
Regresi Linear Sederhana dalam Pemrograman R
Analisis regresi digunakan untuk menganalisis hubungan antar variabel. Pada artikel ini, kita akan membahas cara melakukan analisis regresi dalam pemrograman R.
Analisis regresi merupakan metode yang digunakan untuk menganalisis hubungan antar variabel. Jika hanya terdapat satu variabel independen atau variabel bebas, maka disebut analisis regresi linier sederhana (simple linear regression).
Pada artikel ini, kita akan membahas cara melakukan analisis regresi linear sederhana dalam pemrograman R. Perhatikan contoh berikut.
Seorang manajer di suatu perusahaan ingin mengetahui apakah kompetensi pegawai (X) memengaruhi kinerja pegawai (Y) di perusahaannya. Maka dari itu, diambil sampel acak sebanyak 15 orang pegawai dengan kompetensi dan kinerja sebagai berikut:
| No | X | Y | No | X | Y |
|---|---|---|---|---|---|
| 1 | 40 | 4 | 9 | 30 | 4 |
| 2 | 55 | 16 | 10 | 22 | 14 |
| 3 | 32 | 12 | 11 | 40 | 24 |
| 4 | 55 | 24 | 12 | 64 | 26 |
| 5 | 50 | 15 | 13 | 58 | 20 |
| 6 | 52 | 24 | 14 | 48 | 9 |
| 7 | 61 | 22 | 15 | 44 | 14 |
| 8 | 44 | 17 |
Dari data di atas:
- Buat scatter plot antara kompetensi pegawai dan kinerja pegawai menggunakan R.
- Cari model regresi linear sederhana yang menjelaskan hubungan antara kompetensi pegawai (X) dan kinerja pegawai (y).
Sintaks:
## Input data ##
x <- c(40, 55, 32, 55, 50, 52, 61, 44, 30, 22,
40, 64, 58, 48, 44)
y <- c(4, 16, 12, 24, 15, 24, 22, 17, 4,
14, 24, 26, 20, 9, 14)
## Membuat scatter plot atau diagram pencar
plot(x,y)
## Membuat garis regresi
abline(lm(y~x))
Output:
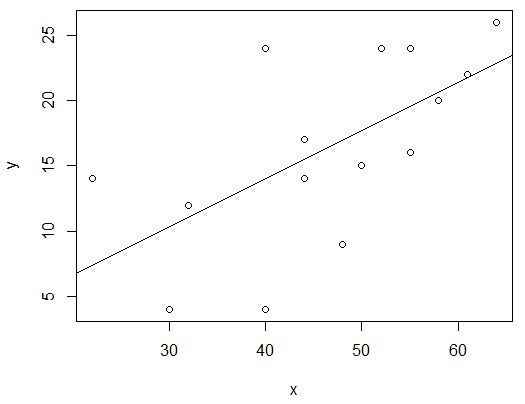
## Mencari persamaan model regresi linear sederhana
lm(y~x)
Output
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-0.6704 0.3670
Berdasarkan output di atas, model regresi linear sederhananya dapat ditulis sebagai berikut:
\[ Y = -0.6704 + 0.367X \]
Perhatikan bahwa koefisien \(X\) pada model regresi yang diperoleh adalah positif. Ini artinya terdapat hubungan yang positif antara kompetensi pegawai (\(X\)) dan kinerja pegawai (\(Y\)). Dengan kata lain, semakin tinggi kompetensi yang dimiliki pegawai, maka semakin baik pula kinerjanya. Hasil ini sesuai dengan diagram pencar yang telah kita peroleh sebelumnya.
Untuk menampilkan ringkasan dari perhitungan regresi, gunakan perintah summary(fit). Perintah summary() ini akan menampilkan tabel anova beserta uji parsial (uji t) dan uji simultan (uji F) lengkap dengan signifikansinya. Selain itu, juga terdapat nilai koefisien determinasi atau \( R^2 \) untuk menentukan kesesuaian model.
Adapun ringkasan dari perhitungan regresi dalam contoh kita dapat dilihat sebagai berikut:
summary(lm(y~x))
Output
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-10.0091 -3.0964 0.2842 3.8347 9.9909
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.6704 6.1418 -0.109 0.9148
x 0.3670 0.1286 2.854 0.0136 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.776 on 13 degrees of freedom
Multiple R-squared: 0.3852, Adjusted R-squared: 0.3379
F-statistic: 8.145 on 1 and 13 DF, p-value: 0.01355
Berdasarkan output di atas, model regresinya bisa dilihat dari bagian estimate, yaitu \( y = -0.6704 + 0.36x \). Dari uji parsial dengan t-value sebesar 2.854 dan p-value 0.0135 di mana tingkat signifikansi yang digunakan adalah 0.05, memberikan hasil tolak \( H_0: \beta_1 = 0 \). Artinya variabel \(X\) (nilai kompetensi pegawai) secara signifikan berpengaruh terhadap model.
Nilai koefisien regresi dari \(X\) sebesar 0.36 dapat kita interpretasikan bahwa setiap kenaikan nilai satu unit \(X\) (nilai kompetensi pegawai), maka nilai \(Y\) (skor kinerja) akan naik sebesar 0.36.
Artikel Terkait
Live in the present and make it so beautiful that it’s worth remembering.
Arnold H. Glasow
