Tutorial R   »   Statistik Nonparametrik   ›  Uji Kruskall-Wallis dalam Pemrograman R

Uji Kruskal Wallis

Uji Kruskall-Wallis dalam Pemrograman R

Uji Kruskal-Wallis merupakan uji statistik nonparametrik untuk \(k\) sampel independen. Untuk melakukan uji Kruskall-Wallis dalam R, kita dapat menggunakan fungsi kruskal.test() pada package stats.

Uji Kruskal-Wallis merupakan uji statistik nonparametrik untuk \(k\) sampel independen. Uji ini digunakan sebagai alternatif ketika ANOVA satu arah dalam statistik parametrik tidak dapat dipakai karena tidak terpenuhinya asumsi yang diharuskan dalam ANOVA satu arah.

Untuk melakukan uji Kruskall-Wallis dalam R, kita dapat gunakan fungsi kruskal.test() pada package stats.

Sebagai contoh, kita akan gunakan data PlantGrowth yang merupakan dataset bawaan R. Data PlantGrowth ini memberikan data hasil percobaan dengan membandingkan hasil penen (yields), yang diukur dengan berat tanaman kering (dried weight of plants), untuk tiga kondisi, yakni di bawah kontrol dan dua perlakuan yang berbeda.

Dataset ini disajikan dalam sebuah data frame dengan 30 baris/cases dan 2 variabel yakni variabel weight (numeric) dan variabel group (factor). Perhatikan sintaks berikut ini.

Sintaks:

                
                  # load packages
                  library(tidyverse)
                  library(ggpubr)
                  library(rstatix)
                
              

                
                  library(dplyr)
                  my_data <- PlantGrowth
                  
                  ### membuat ringkasan statistik
                  group_by(my_data, group) %>%
                    summarise(
                      count = n(),
                      mean = mean(weight, na.rm = TRUE),
                      sd = sd(weight, na.rm = TRUE),
                      median = median(weight, na.rm = TRUE),
                      IQR = IQR(weight, na.rm = TRUE)
                    )
                  
                  Output:
                  `summarise()` ungrouping output (override with `.groups` argument)
                  # A tibble: 3 x 6
                    group count  mean    sd median   IQR
                    (fct) (int) (dbl) (dbl)  (dbl) (dbl)
                  1 ctrl     10  5.03 0.583   5.15 0.743
                  2 trt1     10  4.66 0.794   4.55 0.662
                  3 trt2     10  5.53 0.443   5.44 0.467
                
              

Agar lebih jelas, kita visualisasikan data PlantGrowth ini dalam boxplot. Kita akan menampilkan plot rata-rata dari variabel weight menurut kelompok perlakuan (treatment).

                
                  # Visualisasi data dengan boxplot
                  library("ggpubr")
                  ggboxplot(my_data, x = "group", y = "weight", 
                            color = "group", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
                            order = c("ctrl", "trt1", "trt2"),
                            ylab = "Weight", xlab = "Treatment")
                
              

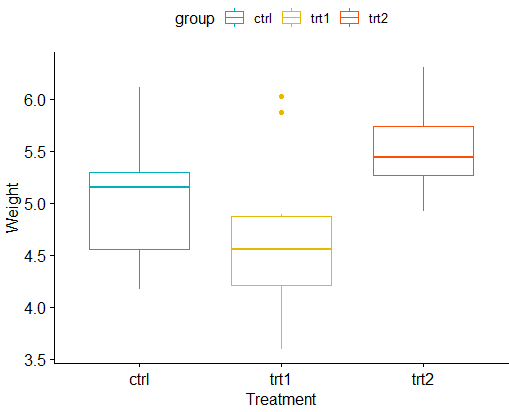
Selain visualisasi boxplot di atas, kita juga bisa menampilkan data melalui plot rata-rata seperti di bawah ini.

                
                  # Mean plots
                  library("ggpubr")
                  ggline(my_data, x = "group", y = "weight", 
                        add = c("mean_se", "jitter"), 
                        order = c("ctrl", "trt1", "trt2"),
                        ylab = "Weight", xlab = "Treatment")
                
              

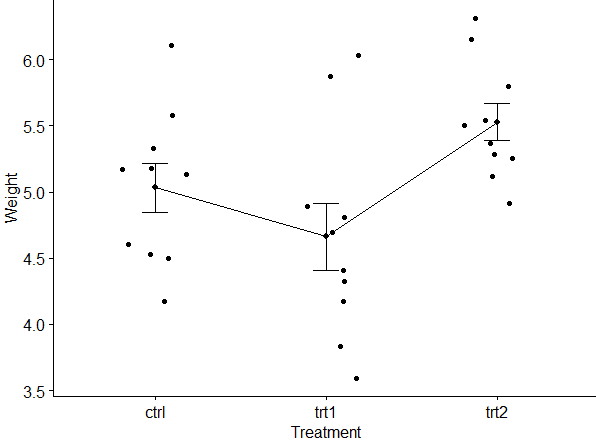
Dari kedua visualisasi data di atas tampak bahwa rata-rata berat (weight) tanaman dengan perlakuan yang kedua (trt2) jauh lebih tinggi dibandingkan rata-rata berat dengan perlakuan pertama (trt1), tetapi tidak jauh berbeda dengan rata-rata berat dengan kondisi dibawah kontrol (ctrl). Selain itu, rata-rata berat dengan perlakuan pertama dan yang dibawah kontrol secara sekilas tampak tidak ada perbedaan yang mencolok.

Untuk mengonfirmasi analisis sederhana kita ini, kita lanjutkan dengan melakukan Uji Kruskal-Wallis.

                
                  # Menghitung Uji Kruskal-Wallis
                  kruskal.test(weight ~ group, data = my_data)
                  
                  Output:
                    Kruskal-Wallis rank sum test

                  data:  weight by group
                  Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842
                
              

Dari output pengujian kruskal-wallis di atas, diperoleh nilai p-value sebesar 0.01842. Nilai ini lebih kecil dari tingkat signifikansi 0.05, sehingga tolak Ho dan disimpulkan bahwa terdapat setidaknya dua variabel berat tanaman yang berbeda dari ketiga kondisi yakni yang dibawah kontrol (ctrl), perlakuan pertama (trt1), dan perlakuan kedua (trt2).

Untuk mengetahui rata-rata berat tanaman mana yang berbeda sesuai ketiga kondisi tersebut, kita lanjutkan dengan melakukan pairwise comparison dengan metode BH seperti tampak di bawah.

                
                  # Multiple pairwise-comparison between groups
                  pairwise.wilcox.test(PlantGrowth$weight, PlantGrowth$group,
                                      p.adjust.method = "BH")
                                      
                  Output:
                    Pairwise comparisons using Wilcoxon rank sum test with continuity correction 

                  data:  PlantGrowth$weight and PlantGrowth$group 

                      ctrl  trt1 
                  trt1 0.199 -    
                  trt2 0.095 0.027

                  P value adjustment method: BH 
                
              

Dari output yang dihasilkan di atas, tampak bahwa rata-rata berat tanaman dengan kondisi perlakuan pertama (trt1) tidak berbeda signifikan dengan rata-rata berat di bawah kondisi kontrol (ctrl) dengan p-value sebesar 0.199. Begitu pula dengan kondisi perlakuan kedua dan yang dibawah kondisi kontrol. Namun, rata-rata berat tanaman yang dihasilkan akibat diberi perlakuan pertama dan kedua tampak berbeda signifikan dengan p-value sebesar 0.027.