Statistik Nonparametrik   »   Kasus Satu Sampel   ›  Uji Run - Rumus dan Contoh Penghitungan

Uji Run

Uji Run - Rumus dan Contoh Penghitungan

Uji run digunakan untuk menguji apakah sederetan data yang terdiri dari dua kategori tersusun secara acak/random atau tersusun secara sistematik.

---

Keacakan (randomness) data dari suatu sampel merupakan syarat yang harus dipenuhi dalam pengambilan sampel suatu populasi. Oleh karena itu, diperlukan uji untuk mengetahui keacakan suatu data. Uji Run digunakan untuk menguji apakah sederetan data yang terdiri dari dua kategori tersusun secara acak/random atau sistematik.

Misalkan kita akan menguji apakah deretan orang yang membeli karcis berikut (laki-laki/L dan perempuan/P) tersusun secara random atau tidak.

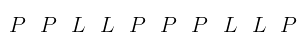
Untuk menjelaskan uji run ini, mari kita tuliskan tanda ( + atau - ) berdasarkan data yang diberikan. Tentu saja kita bisa menggunakan tanda lainnya sesuai keinginan.

Sekarang kita definisikan run sebagai urutan tanpa ganggunan dari satu simbol atau atribut. Selanjutnya, kita definisikan panjang run sebagai banyaknya elemen yang ada di dalamnya.

Dengan demikian, deretan di atas terdiri dari 5 run \((R)\), yaitu diperoleh dari susunan yang berjenis kelamin sama: run pertama ada dua P, run kedua ada dua L, run ketiga ada tiga P, run keempat ada 2 L, run kelima dengan 1 P.

Uji Run Sampel Kecil (\(n_1\) dan \(n_2 \leq 20\))

Untuk uji run sampel kecil atau kurang dari sama dengan 20, pergunakan tabel run-F1 (batas minimum) dan tabel run-F2 (batas maksimum) dalam penentuan penolakan \(H_0\). Tabel run-F (Siegel, 1997) memberikan nilai kritis \(R\) di bawah \(H_0\) untuk \(α = 0,05\).

Jika nilai \(R_{\text{obs}}\) jatuh di antara nilai kritis yang diberikan Tabel \(F_1\) dan \(F_2\) \( (F_1 < R_{\text{obs}} < F_2) \), maka \(H_0\) diterima. Jika nilai \(R_{\text{obs}} ≤ \) nilai kritis dari tabel \(F_1\) atau \(R_{\text{obs}} ≥ \) nilai kritis dari tabel \(F_2\), maka \(H_0\) ditolak.

Uji Sampel Besar (\(n_1\) atau \(n_2 > 20\))

Untuk sampel besar, distribusi dari sampel \(R\) (run) mendekati distribusi normal \(Z\) dengan rata-rata \(μ_r\) dan varians \(σ_r^2\).

di mana:

Prosedur Melakukan Uji Run

Langkah-langkah dalam menggunakan uji run adalah:

1. Tentukan hipotesis nol (H0), hipotesis alternatif (H1) dan taraf signifikansinya (α)
2. Susunlah observasi-observasi n1 dan n2 menurut urutan terjadinya; kemudian hitunglah banyaknya run (r) berdasarkan pengamatan yang terjadi;
3. Hitunglah kemungkinan di bawah H0 yang dikaitkan dengan suatu nilai yang seekstrem r yang diobservasi. Jika probabilitas (p-value) itu sama atau kurang dari α, tolaklah H0. Nilai p-value bergantung pada ukuran n1 dan n2, yakni:
1. Jika n1 dan n2 ≤20, pakailah Tabel run-F untuk α=0,05.

Tabel F1 menyajikan nilai-nilai r yang sedemikian kecilnya sehingga kemungkinannya di bawah H0.

Tabel F2 menyajikan nilai-nilai r yang sedemikian besarnya sehingga kemungkinannya di bawah H0

2. Jika (n1 dan n2 > 20), hitunglah Z dengan menggunakan rumus (2) di atas, lalu lihat tabel normal.
4. Keputusan: Jika p-value yang didapat sama atau kurang dari α, maka H0 ditolak.
5. Kesimpulan

Contoh 1: Sampel Besar (\(n_1\) atau \(n_2 > 20\))

Seorang peneliti ingin mengetahui apakah pengaturan antrian pria dan wanita di depan box pembelian tiket teater mengikuti pengaturan random. Data diperoleh dengan melakukan tally jenis kelamin dari urutan 50 orang yang menuju box pembelian tiket. Urutan dari 30 pria (P) dan 20 wanita (W) adalah sebagai berikut:

Pembahasan:

Hipotesis:

H₀ : Urutan pria dan wanita dalam antrian adalah random

H₁ : Urutan pria dan wanita dalam antrian tidak random

Tingkat Signifikansi: \(\alpha = 0,05 \)

Uji Statistik:

Karena bertujuan untuk menguji kerandoman data yang berasal dari sampel tunggal dan datanya berskala nominal, maka uji yang dipilih adalah uji run sampel tunggal.

Diketahui N = 50, P = 30, W = 20, dan R_obs = 35. Untuk sampel besar maka menggunakan pendekatan distribusi normal.

Karena H1 tidak memprediksi arah dari kerandoman, maka digunakan uji dua arah. Sehingga daerah penolakan mencakup nilai Z_(α/2) di luar ± 1,96; atau jika (p-valuetabel normal x 2) ≤ α_sig maka Tolak H₀

Keputusan:

Karena Z_obs = 2,98 > Z_(α/2) = 1,96; maka tolak H₀. Atau karena (p-valuetabel normal x 2) = 0,0014 x 2 ≤ α_sig = 0,05; maka tolak H₀.

Kesimpulan: Dengan tingkat signifikansi 5%, dapat disimpulkan bahwa urutan pria dan wanita dalam antrian adalah tidak acak.

Sumber:

Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama