Statistik Nonparametrik   »   Kasus Banyak Sampel Independen   ›  Uji Kruskal Wallis - Rumus dan Contoh Penghitungan

Uji Kruskal Wallis

Uji Kruskal Wallis - Rumus dan Contoh Penghitungan

Uji Kruskal Wallis digunakan sebagai alternatif ketika ANOVA satu arah dalam statistik parametrik tidak dapat dipakai karena tidak terpenuhinya asumsi yang diharuskan dalam ANOVA satu arah.

---

Uji Kruskal-Wallis merupakan uji statistik nonparametrik untuk \(k\) sampel independen. Uji ini digunakan sebagai alternatif ketika ANOVA satu arah dalam statistik parametrik tidak dapat dipakai karena tidak terpenuhinya asumsi yang diharuskan dalam ANOVA satu arah.

Hipotesis nol dari uji kruskal-wallis menyatakan bahwa \(k\) sampel berasal dari populasi yang sama atau dari populasi yang identik, sedangkan hipotesis alternatifnya bisa ditulis minimal ada sampel berasal dari populasi yang berbeda. Dalam menguji hipotesis nol nya diasumsikan variabel yang diteliti berdistribusi kontinu.

Metodologi

Dalam penerapan uji kruskal-wallis, nilai setiap sampel \((X_{ij})\) diletakkan pada tabel yang tiap kolomnya mewakili sampel atau kelompok \((k)\). Data yang sudah tertata akan menjadi tabel seperti berikut.

Tabel 1. Tampilan data hasil observasi atau pengamatan

Keterangan: \(X_{ij}\) adalah data untuk observasi ke-i pada kelompok ke-j dan \(n_j\) adalah jumlah observasi pada kelompok ke-j. Besarnya \(n\) untuk setiap sampel/kelompok tidak harus sama.

Pada perhitungan uji Kruskal-Wallis, semua nilai/skor dari seluruh \(k\) sampel disatukan dan diranking secara menyeluruh dalam satu sistem perankingan. Nilai terkecil diberi ranking 1, nilai terkecil ke-2 diberi ranking 2, dan seterusnya sampai nilai terbesar diberi ranking \(N\), di mana \(N\) adalah jumlah total observasi independen pada \(k\) sampel atau banyak sampel dalam semua populasi.

Setelah selesai melakukan perankingan, jumlahkan ranking dalam setiap kolom. Jika sampel berasal dari populasi yang sama atau identik, rata-rata ranking setiap kolom seharusnya sama secara statistik. Kalau sampel berasal dari populasi yang berbeda, maka rata-rata rankingnya akan berbeda. Untuk menghitung statistik Kruskal-Wallis berikut rumusnya:

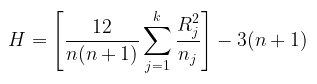
Rumus yang ekivalen dengan di atas adalah

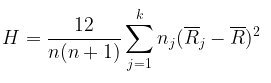
di mana:

\(k\) = banyak kelompok

\(n_j\) = banyak sampel ke-j

\(n\) = banyak sampel dalam semua populasi atau total nj

\(R_j\) = jumlah ranking pada populasi ke-j (j = 1, 2, ... , k)

\( \overline{R} = (n+1)/2 \) = rata-rata ranking sampel gabungan

\( \overline{R}_j \) = rata-rata ranking ke-j

Ketika terdapat dua atau lebih nilai yang sama (tidak harus dalam satu kelompok), maka setiap nilai yang sama tersebut diberi ranking rata-rata (seperti pada prosedur ranking Spearman). Untuk mengoreksi efek dari ranking kembar, maka dihitung statistik Kruskal-Wallis (H) yang menggunakan faktor koreksi, yaitu dengan membagi nilai statistik Kruskal-Wallis dengan:

di mana:

\(g\) = banyaknya ranking yang kembar

\(t_i\) = banyak ranking kembar di kelompok ke-i

\(n\) = banyaknya sampel dalam semua populasi atau total ni

Dengan demikian rumus statistik Kruskal-Wallis yang memasukkan faktor koreksi menjadi:

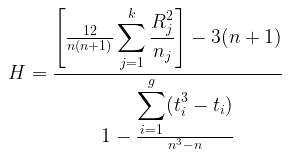
Prosedur Uji Kruskal-Wallis

Berikut adalah prosedur untuk melakukan Uji Kruskal-Wallis:

1. Tentukan hipotesis penelitian. \(H_0\): sampel berasal dari populasi yang sama. \(H_1\): sampel berasal dari populasi yang berbeda (minimal ada satu yang berbeda).
2. Tentukan tingkat signifikansi \((α)\)
3. Hitung statistik uji \((H)\). Masukkan nilai-nilai hasil observasi ke dalam tabel \(k\) kolom lalu rangking seluruh nilai tersebut dari 1 sampai \(N\) (dari nilai terkecil ke nilai terbesar). Kemudian, hitung statistik hitung Cochran Q berdasarkan rumus yang diberikan di atas.
4. Tentukan wilayah kritisnya.
5. Keputusan: Tolak \(H_0\) jika \(H ≥ χ^2\) tabel. Untuk sampel kecil \((k = 3)\) dan \((n_j ≤ 5)\) lihat Tabel Kruskal-Wallis. Sedangkan untuk sampel besar \((n_j>5)\), pakai Tabel Chi Square dengan \(db = k – 1\).
6. Buatlah kesimpulan dari hasil yang diperoleh.

Contoh Soal 1:

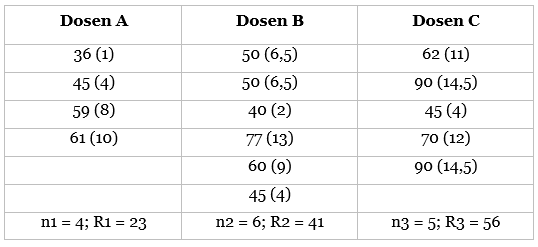
Seorang peneliti ingin mengetahui apakah terdapat perbedaan prestasi belajar mahasiswa yang diajar oleh dosen A, dosen B, dan dosen C. Berdasarkan data berikut, apakah dapat disimpulkan bahwa terdapat perbedaan prestasi belajar antara mahasiswa yang diajar oleh dosen A, B, dan C? (Ujilah dengan alpha = 5%).

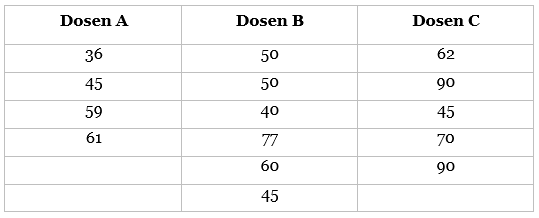
Pembahasan:

Tentukan hipotesis:

Tentukan hipotesis penelitian. \(H_0\): Prestasi belajar mahasiswa untuk ketiga dosen sama. \(H_1\): Prestasi belajar mahasiswa untuk ketiga dosen berbeda (miniam ada satu yang berbeda)

Taraf signifikansi: alpha = 5%.

Statistik Uji:

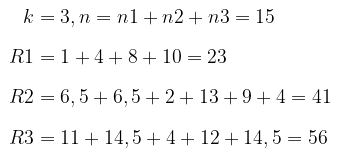
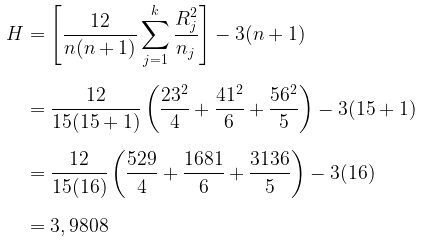
Karena terdapat ranking kembar, maka gunakan faktor koreksi, yakni

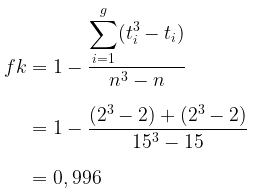
Dengan demikian, statistik hitung Kruskal-Wallis menjadi:

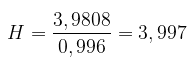
Wilayah kritis: Dengan alpha = 5% dan \(db = 3-1 = 2\) didapat \(H\) tabel = 5,991 (lihat tabel \(χ^2)\).

Keputusan: Karena \(H\) hitung < \(H\) tabel, maka \(H_0\) tidak ditolak.

Kesimpulan: Dengan tingkat kepercayaan 95% dan berdasarkan sampel yang ada, dapat disimpulkan bahwa terdapat cukup bukti untuk menyatakan prestasi belajar mahasiswa yang diajar oleh ketiga dosen berbeda (minimal ada satu yang berbeda).

Sumber:

Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama