
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA NONPARAMETRIK
Statistik Nonparametrik
Pendahuluan
Kasus Satu Sampel
Kasus Dua Sampel Independen
Kasus Dua Sampel Berhubungan
Kasus Banyak Sampel Independen
Kasus Banyak Sampel Berhubungan
Koefisien Korelasi (Korelasi Nonparametrik)
Statistik Nonparametrik » Kasus Banyak Sampel Berhubungan › Uji Friedman - Rumus dan Contoh Penghitungan
Uji Friedman
Uji Friedman - Rumus dan Contoh Penghitungan
Uji Friedman digunakan sebagai alternatif ANOVA dua arah dalam statistik parametrik ketika asumsi dalam ANOVA dua arah tidak dapat terpenuhi.
Uji Friedman merupakan uji statistik nonparametrik untuk \(k\) sampel berhubungan atau berpasangan. Uji ini digunakan sebagai alternatif ketika ANOVA dua arah dalam statistik parametrik tidak dapat dipakai karena tidak terpenuhinya asumsi yang diharuskan dalam ANOVA dua arah. Tujuan uji ini adalah untuk melihat apakah ada perbedaan pengaruh antar perlakuan.
Metodologi
Skor-skor hasil pengamatan dituliskan ke dalam tabel dua arah yang memiliki k kolom dan n baris.
Tabel 1. Tampilan data hasil observasi atau pengamatan

di mana:
\(X_{ij}\) = nilai ranking untuk sampel ke-i dalam perlakuan ke-j
\(R_j\) = jumlah ranking sampel dalam perlakuan ke-j
\(i\) = banyaknya kelompok/sampel = 1, 2, 3, . . . , n
\(j\) = banyaknya perlakuan = 1, 2, 3, . . ., k
Rumus statistik uji Friedman adalah

Apabila terdapat ranking yang kembar atau sama (hanya angka sama yang terjadi dalam suatu kelompok saja yang patut dipermasalahkan), maka rumus Friedman dibagi dengan
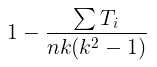
di mana: \( T_i = \sum (t_i^3 - t_i) \), dan \(t\) = banyaknya nilai pengamatan yang sama untuk suatu subjek dalam kelompok ke-i.
Dengan demikian, rumus Friedman apabila terdapat ranking yang sama dapat dituliskan menjadi:
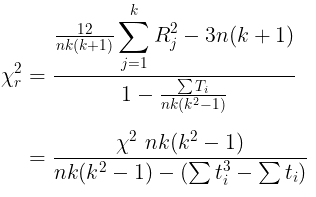
Hal yang perlu diingat ialah bahwa \( \chi^2_r \) mendekati distribusi chi-square dengan \(db = k - 1\) hanya bila banyak baris dan/atau kolom tidak terlalu kecil. Jika banyak baris atau kolom kurang dari minimal, gunakan tabel peluang dua arah Friedman untuk membuat keputusan penolakan dan penerimaaan hipotesis nol.
Prosedur Uji Friedman
- Tentukan hipotesis nol dan hipotesis alternatif. \(H_0\): Sampel berasal dari populasi yang sama \((M_1 = M_2 = ... = M_k)\). \(H_1\): Sampel berasal dari populasi yang berbeda (paling tidak ada 1 yang berbeda).
- Tentukan taraf signifikansi yang digunakan \((α)\).
- Hitung statistik uji: Skor-skor hasil pengamatan dituliskan ke dalam tabel dua arah yang memiliki \(k\) kolom dan \(n\) baris. Pada masing-masing kolom, semua ranking dijumlahkan untuk mendapatkan ranking pada masing-masing kolom, \(R_j\). Setelah itu, hitunglah statistik uji Friedman seperti diberikan pada rumus di atas.
- Tentukan wilayah kritis. Untuk \(k\) dan \(n\) kecil gunakan Tabel Dua Arah Friedman untuk penentuan wilayah kritis. Jika \(k\) dan \(n\) cukup besar, gunakan chi-square.
- Keputusan: Tolak \(H_0\) jika \( \chi^2_r \) hitung > \( \chi^2_r \) tabel atau jika \(p-value < α\).
- Buat kesimpulan dari hasil yang diperoleh.
Contoh Soal 1:
Restoran LEZAT ingin meluncurkan empat paket masakan dengan nama paket 1, paket 2, paket 3 dan paket 4. Untuk mengetahui bagaimana tanggapan konsumen terhadap keempat paket tersebut, sejumlah 10 orang (sampel) dipersilakan mencicipi keempat jenis paket tersebut, kemudian memberikan penilaian kepada tiap-tiap paket. Nilai yang diberikan ditentukan antara 0 sampai dengan 100.
Berikut adalah hasil penilaian kesepuluh orang terhadap paket yang ditawarkan.
| Responden | PAKET 1 | PAKET 2 | PAKET 3 | PAKET 4 | |
|---|---|---|---|---|---|
| 1 | 80 | 75 | 72 | 82 | |
| 2 | 85 | 78 | 68 | 84 | |
| 3 | 82 | 82 | 64 | 71 | |
| 4 | 81 | 86 | 82 | 76 | |
| 5 | 84 | 71 | 88 | 70 | |
| 6 | 83 | 79 | 86 | 89 | |
| 7 | 89 | 80 | 80 | 90 | |
| 8 | 84 | 82 | 74 | 74 | |
| 9 | 72 | 84 | 76 | 71 | |
| 10 | 75 | 70 | 81 | 72 |
Akan diteliti apakah keempat paket tersebut mempunyai mutu (dalam hal ini nilai) yang sama?
Pembahasan:
Di sini seorang responden (penilai) mencicipi keempat jenis paket masakan tersebut, atau bisa dikatakan suatu eksperimen yang pengukurannya terhadap keempat paket masakan dilakukan terhadap subjek yang sama (seorang responden/penilai). Oleh karena paket masakan lebih dari dua, maka pengujian bisa dilakukan secara uji lebih dari dua sampel berhubungan.
Hipotesis:
\(H_0\): Populasi-populasi dalam suatu blok adalah identik (Keempat jenis paket mempunyai mutu/penilaian yang sama).
\(H_1\): Sekurang-kurangnya salah satu perlakuan cenderung menghasilkan output yang lebih besar dibandingkan dengan sekurang-kurangnya salah satu perlakuan lain. Atau, dalam kasus di atas sekurang-kurangnya salah satu jenis paket mendapat penilaian yang lebih besar dibandingkan dengan sekurang-kurangnya salah satu paket yang lainnya.
Tingkat Signifikansi: \(\alpha = 5\%\)
Statistik uji:
Berdasarkan data hasil penilaian yang diberikan pada soal, buatlah ranking setiap perlakuan untuk setiap subjek/orang. Tabel berikut menunjukkan hasil perankingan yang telah dilakukan.
| Responden | PAKET 1 | PAKET 2 | PAKET 3 | PAKET 4 | |
|---|---|---|---|---|---|
| 1 | 3 | 2 | 1 | 4 | |
| 2 | 4 | 2 | 1 | 3 | |
| 3 | 3,5 | 3,5 | 1 | 2 | |
| 4 | 2 | 4 | 3 | 1 | |
| 5 | 3 | 2 | 4 | 1 | |
| 6 | 2 | 1 | 3 | 4 | |
| 7 | 3 | 1,5 | 1,5 | 4 | |
| 8 | 4 | 3 | 1,5 | 1,5 | |
| 9 | 2 | 4 | 3 | 1 | |
| 10 | 3 | 1 | 4 | 2 | |
| \(R_j\) | 29,5 | 24 | 23 | 23,5 |
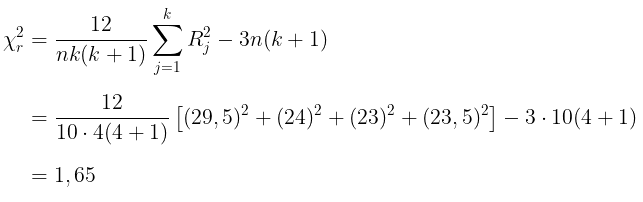
Karena kita menjumpai angka yang sama, yakni ada 2 skor 74, 2 skor 80, dan 2 skor 82, maka \( \chi^2_r \) harus dikoreksi. Kita peroleh sebagai berikut.

Dengan demikian, statistik hitung Friedman yang telah dikoreksi menjadi:
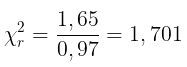
Selanjutnya, dari tabel chi-square dengan tingkat signifikansi 5% dan derajat bebas \(db = k - 1 = 4 - 1 = 3\), diperoleh nilai chi-square tabel sebesar 7,82.
Keputusan: Karena nilai chi-square hitung lebih kecil dibandingkan nilai chi-square tabel, yakni \(1,701 < 7,82\), maka gagal tolak \(H_0\).
Kesimpulan: Dengan tingkat signifikansi 5%, dapat disimpulkan bahwa keempat jenis paket mempunyai penilaian yang relatif sama.
Sumber:
Siegel, Sidney. 1997. Statistika Nonparametrik untuk Ilmu-ilmu Sosial. Jakarta: PT Gramedia Pustaka Utama
Artikel Terkait
Only those who can see the invisible can accomplish the impossible.
Patrick Snow