MPC I   »   Simple Random Sampling   ›  Penggunaan Tabel Angka Random untuk Pemilihan Unit dalam Simple Random Sampling

Sampling

Penggunaan Tabel Angka Random untuk Pemilihan Unit dalam Simple Random Sampling

Salah satu metode yang dapat digunakan untuk pemilihan unit dalam penarikan sampel acak sederhana adalah dengan menggunakan tabel angka random (random number table).

---

Simple random sampling (SRS) atau penarikan sampel acak sederhana (PSAS) adalah teknik memilih sampel dari suatu populasi sedemikian rupa sehingga setiap anggota populasi mempunyai peluang yang sama untuk terambil sebagai sampel.

Salah satu metode yang dapat digunakan untuk pemilihan unit dalam PSAS adalah dengan menggunakan tabel angka random (random number table). Contoh salah satu halaman pada Tabel Angka Random (TAR) diberikan di bawah ini. Setiap blok baris dari TAR ini terdiri dari lima kolom. Misal blok kolom pertama terdiri dari angka 8,8,3,4 dan 7, dan blok kolom ketiga terdiri dari angka 7,8,6,0, dan 7.

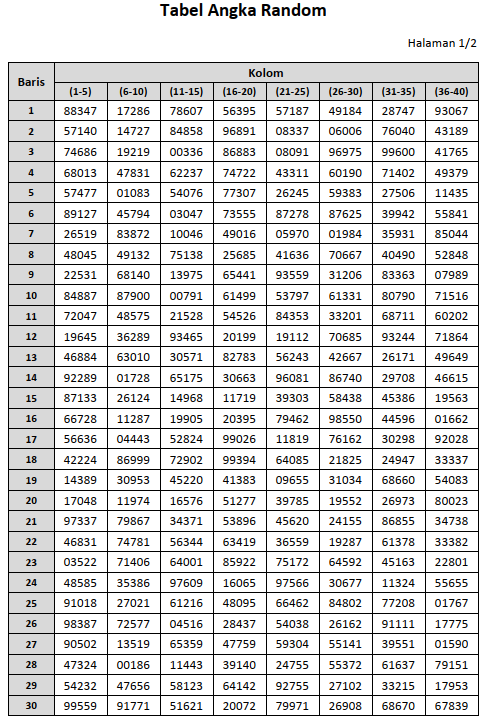
Download tabel angka random: tabel angka random

Ada tiga pendekatan dalam menggunakan tabel angka random yakni: (a) Remainder Approach, (b) Quotient Approach dan (c) Independent Choice of Digits. Kita akan membahasnya satu per satu berikut ini.

Independent Choice of Digits

Berikut adalah langkah-langkah pemilihan unit sampel mengunakan pendekatan independent choice of digits:

1. Tentukan halaman tabel angka random (TAR) yang akan digunakan, kemudian pilih baris dan kolom dari halaman TAR yang terpilih untuk memulai penelurusan angka random (AR). Anda dapat gunakan hari, tanggal, dan bulan untuk melakukan ini. Misalnya, untuk hari ganjil (senin, rabu, jumat, minggu) maka halaman 1 TAR yang terpilih, dan untuk hari genap (selasa, kamis, sabtu), maka halaman 2 TAR yang terpilih. Lalu, tanggal dapat dijadikan sebagai baris dan bulan sebagai kolom.
2. Jika jumlah populasi sebanyak N unit dan jumlah digits dari N adalah sebanyak r digits, maka telusuri r digit angka dari baris dan kolom permulaan.
3. Jika angka random (AR) ≤ N, maka unit yang nomor urutnya sama dengan AR tersebut terpilih sebagai sampel.
4. Jika angka random (AR) = 0, maka unit ke-N (terakhir) terpilih sampel
5. Jika angka random (AR) > N, maka lanjutkan penelusuran ke angka random di baris selanjutnya pada kolom yang sama. Apabila sudah sampai pada kolom terakhir dan belum juga mendapatkan angka random sebanyak sampel, lanjutkan ke kolom berikutnya pada baris pertama.
6. Lakukan pengambilan AR sampai jumlah sampel yang diinginkan terpenuhi.

Contoh 1: Independent Choice of Digits

Misalkan kita ingin mengambil sampel SRS sebanyak n = 6 dari populasi N = 60. Untuk tujuan keseragaman dan mempermudah penjelasan, pembacaan TAR di sini akan dimulai dari halaman 1, baris 1, dan kolom 1.

Diketahui N = 60, maka jumlah digit populasi adalah 2 (r = 2) sehingga kita mengambil 2 kolom dimulai dari baris pertama, kemudian dilanjutkan ke baris berikutnya pada kolom yang sama sampai sampel yang diinginkan terpilih.

Sampel yang terpilih yaitu sebagai berikut:

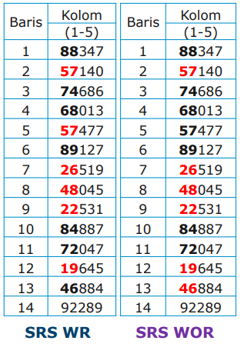
1. untuk WR: 57, 57, 26, 48, 22, 19
2. untuk WOR: 57, 26, 48, 22, 19, 46

Berikut adalah ilustrasinya:

Remainder Approach

Misalkan ada N unit populasi dan jumlah digits dari N adalah sebanyak r digit. Berikut adalah langkah-langkah pemilihan unit sampel menurut Ramainder Approach:

1. Tentukan nilai N’ yaitu kelipatan terbesar dari N dengan jumlah digit yang sama. N’ adalah batas atas dari angka random yang akan terpilih. Sebagai contoh, misalkan diketahui N = 32 maka r = 2, sehingga N’ = 96.
2. Jika AR ≤ N, maka unit yang nomor urutnya sama dengan AR tersebut terpilih sebagai sampel.
3. Jika AR = 0, maka unit ke-N (terakhir) terpilih sebagai sampel.
4. Jika N < AR ≤ N', maka lakukan operasi pembagian:

\[ \frac{AR}{N} = k \ \text{(sisa s)} \]

Unit dengan nomor urut = s akan terpilih sebagai sampel. Jika s = 0, unit ke-N (terakhir) terpilih sampel.

5. Jika AR > N’, maka lanjutkan penelusuran ke angka random di baris selanjutnya pada kolom yang sama.
6. Lakukan pengambilan AR sampai jumlah sampel terpenuhi. Jika sudah sampai kolom terakhir dan belum mendapatkan AR sebanyak sampel, lanjutkan ke kolom berikutnya pada baris pertama.

Contoh 2: Remainder Approach

Misalkan kita ingin mengambil sampel SRS WOR sebanyak n = 3 dari populasi N = 36 dengan metode remainder approach. Untuk tujuan keseragaman dan mempermudah penjelasan, pembacaan TAR di sini dimulai dari halaman 1, baris 1, dan kolom 2.

Karena N = 36, maka r = 2 dan N’=72. Dengan demikian, angka random yang diperoleh beserta apakah angka random tersebut ditolak atau digunakan, diberikan sebagai berikut:

• 83 → Tolak, karena lebih dari N’
• 71 → 71/36 = 1 → sisa 35 (unit ke-35 terpilih sebagai sampel)
• 46 → 46/36 = 1 → sisa 10 (unit ke-10 terpilih sebagai sampel)
• 80 → Tolak, karena lebih dari N’
• 74 → Tolak, karena lebih dari N’
• 91 → Tolak, karena lebih dari N’
• 65 → 65/36 = 1 → sisa 29 (unit ke-29 terpilih sebagai sampel)

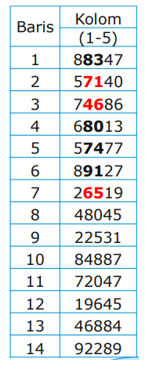
Jadi, sampel yang terpilih adalah sampel dengan nomor urut 35, 10 dan 29.

Quotient Approach

Misalkan terdapat N unit populasi dan jumlah digits dan N adalah sebanyak r digit. Berikut adalah langkah-langkah pengambilan unit sampel menurut Quotient Approach:

1. Tentukan nilai N’ yaitu kelipatan terbesar dari N dengan jumlah digit yang sama. Misalkan N = 32, maka r = 2 dan N’=96.
2. Angka random (AR) yang diambil adalah mulai dari 0 sampai (N’-1).
3. Hitung nilai q = N’/N dan t = AR/q (pembulatan ke bawah). Sampel terpilih = unit dengan nomor urut (t-1).
4. Lakukan pengambilan AR sampai jumlah sampel terpenuhi. Jika sudah sampai baris terakhir di kolom tersebut dan belum mendapatkan AR sebanyak sampel, lanjutkan ke kolom berikutnya baris pertama.

Contoh 3: Quotient Approach

Misalkan kita ingin mengambil sampel SRS WOR di mana n = 3 dari populasi N = 36 dengan quotient approach. Untuk tujuan keseragaman, pembacaan TAR dimulai dari halaman 1, baris 1, dan kolom 2.

Karena N = 36, maka r = 2 dan N’= 72; N’-1 = 71; q = 72/36 = 2. Angka random terpilih beserta apakah angka random tersebut ditolak atau dipakai ditunjukkan berikut ini:

• 83 → Tolak, karena lebih dari N’ - 1
• 71 → t = 71/q = 71/2 = 35 (unit ke-34 terpilih sebagai sampel)
• 46 → t = 46/q = 46/2 = 23 (unit ke-22 terpilih sebagai sampel)
• 80 → Tolak, karena lebih dari N’ - 1
• 74 → Tolak, karena lebih dari N’ - 1
• 91 → Tolak, karena lebih dari N’ - 1
• 65 → 65/q = 65/2 = 32 (unit ke-31 terpilih sebagai sampel)

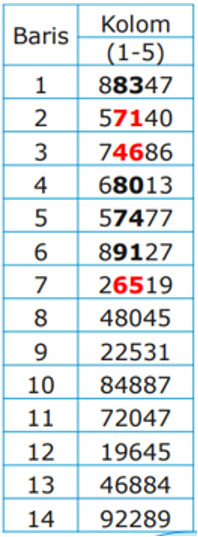
Jadi, sampel terpilih adalah sampel dengan nomor urut 34, 22, 31.