MPC I   »   Simple Random Sampling   ›  Estimasi Rata-rata dan Total Populasi dalam SRS WOR

Sampling

Estimasi Rata-rata dan Total Populasi dalam SRS WOR

Setelah sampel diperoleh, langkah berikutnya adalah melakukan pendugaan untuk memperoleh parameter atau karakteristik populasi. Pada artikel ini, akan dibahas pendugaan rata-rata dan total populasi dengan SRS tanpa pengembalian (SRS-WOR).

---

Pada artikel sebelumnya, kita telah membahas secara singkat mengenai metode penarikan sampel acak sederhana (PSAS) atau simple random sampling (SRS) dan prosedur pemilihan unit dalam SRS. Setelah sampel diperoleh, langkah berikutnya adalah melakukan pendugaan untuk memperoleh parameter atau karakteristik populasi. Pada artikel ini, akan dibahas pendugaan rata-rata dan total populasi dengan SRS tanpa pengembalian (SRS-WOR).

Pendugaan Rata-rata Populasi, μ dan \(\overline{Y}\)

Misalkan terdapat populasi dengan nilai-nilainya yaitu \( Y_1, Y_2, \cdots Y_N \). Kemudian dilakukan penarikan sampel secara acak sederhana tanpa pengembalian (SRS WOR), sehingga diperoleh sampel yang mengandung nilai \(y_1, y_2,…,y_n\). Statistik rata-rata dan varians yang diperoleh berdasarkan data sampel adalah nilai penduga bagi rata-rata (μ) dan varians populasinya (σ).

Dengan demikian, penduga tak bias (unbiased estimator) bagi rata-rata populasi (μ) adalah sebagai berikut:

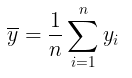
dengan variansnya adalah

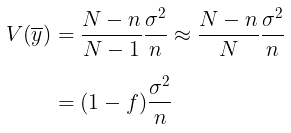
di mana (1-f) biasa disebut dengan istilah finite population correction (fpc). Karena \(\sigma^2\) sering kali tidak diketahui, maka perkiraan varians dan standard error-nya diberikan oleh:

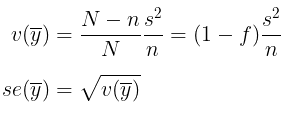
di mana:

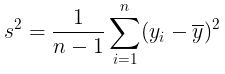
Dengan demikian, (1-α)% confidence interval atau tingkat keyakinan untuk μ adalah:

1. jika populasi normal dan \(\sigma^2\) diketahui, maka

2. jika populasi normal dan \(\sigma^2\) tidak diketahui, diperkirakan dengan \(s^2\), maka

3. jika diasumsikan bentuk distribusi populasi tidak diketahui, tetapi \(\sigma^2\) diketahui dan n mendekati tak berhingga (biasanya digunakan patokan lebih atau sama dengan 30, atau ada juga yang berpendapat lebih atau sama dengan 50), maka

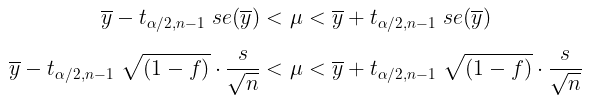
Pendugaan Total Nilai Populasi \(\hat{Y}\)

Selain rata-rata populasi, yang biasa dilakukan juga adalah menduga total nilai suatu karakteristik tertentu dalam populasi berdasarkan sampel, yaitu dengan rumus sebagai berikut:

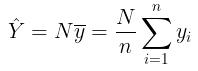
dengan variansnya adalah:

Karena \(\sigma^2\) biasanya tidak diketahui, maka perkiraan varians dan standard error-nya diberikan oleh:

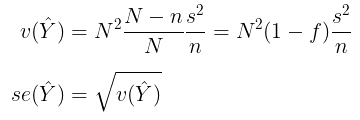
Dengan demikian, tingkat keyakinan (confidence interval) (1-α)% untuk Y adalah:

1. jika populasi normal dan \(\sigma^2\) diketahui,

2. jika populasi normal dan \(\sigma^2\) tidak diketahui, diperkirakan dengan \(s^2\),

3. jika diasumsikan bentuk distribusi populasi tidak diketahui, tetapi \(\sigma^2\) diketahui dan n mendekati tak berhingga (biasanya digunakan patokan lebih atau sama dengan 30, atau ada juga yang berpendapat lebih atau sama dengan 50),

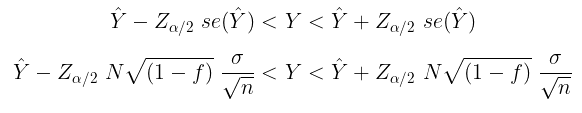
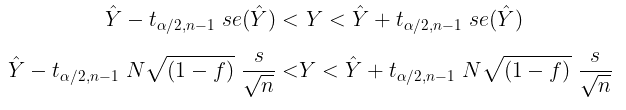
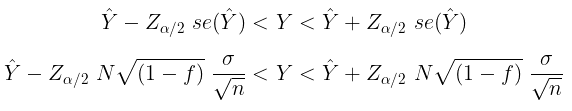
Contoh 1:

Sebuah sampel acak/random sederhana tanpa pengembalian (PSAS-TP) (SRS-WOR) sebanyak 15 rumah tangga dipilih dari 120 rumah tangga di sebuah wilayah. Kemudian dicatat jumlah anggota rumah tangga pada masing-masing rumah tangga (y) dan datanya adalah sebagai berikut:

Perkirakan total penduduk yang ada di wilayah tersebut dalam sebuah tingkat keyakinan (confidence interval) 95%! Diasumsikan bahwa sebaran banyaknya anggota rumah tangga mengikuti sebaran Normal.

Pembahasan:

Diketahui bahwa N = 120; n = 5. Dengan demikian, perkiraan rata-rata anggota rumah tangga per rumah tangga adalah:

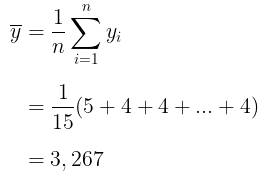
Jadi, rata-rata ada sekitar 3,3 orang (3 sampai 4 orang) per rumah tangga. Selanjutnya, untuk menentukan perkiraan varians dari rata-rata sampel kita hitung nilai \(s^2\) terlebih dahulu:

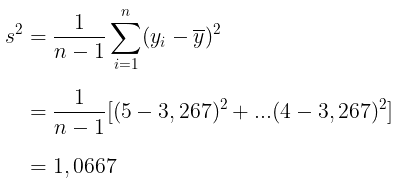
Jadi, perkiraan varians dari rata-rata sampel adalah:

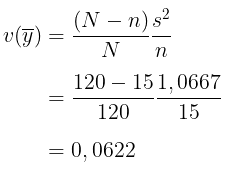
Selanjutnya, perkiraan penduduk di wilayah tersebut adalah:

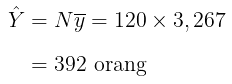
dengan perkiraan varians dan standard error dari perkiraan total penduduk di wilayah tersebut adalah:

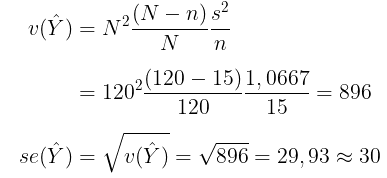
Dengan demikian, pendugaan interval total penduduk di wilayah tersebut dengan tingkat keyakinan 95% adalah sebagai berikut:

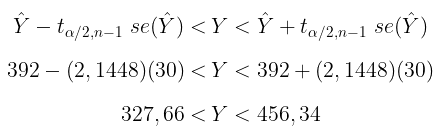
Dengan kata lain, pendugaan interval untuk total penduduk di wilayah tersebut dengan tingkat keyakinan 95% adalah 328 jiwa < Y < 457 jiwa.

Sumber:

Asra, Abuzar & Achmad Prasetyo. 2015. Pengambilan Sampel dalam Penelitian Survei. PT RajaGrafindo Persada: Jakarta.