MPC I   »   Simple Random Sampling   ›  Estimasi Proporsi atau Persentase Populasi dalam SRS WOR

Sampling

Estimasi Proporsi atau Persentase Populasi dalam SRS WOR

Pendugaan proporsi biasa digunakan ketika datanya dalam bentuk variabel kualitatif yang berskala nominal atau ordinal. Misalnya kita ingin mengetahui berapa proporsi perokok yang menderita kanker paru-paru. Dalam hal ini, variabel penelitian berupa data kualitatif dengan kategori 'perokok penderita kanker paru-paru' dan 'perokok yang tidak menderita kanker paru-paru'.

---

Pendugaan proporsi biasa digunakan ketika datanya dalam bentuk variabel kualitatif yang berskala nominal atau ordinal. Misalnya kita ingin mengetahui berapa proporsi perokok yang menderita kanker paru-paru. Dalam hal ini, variabel penelitian berupa data kualitatif dengan kategori 'perokok penderita kanker paru-paru' (bisa dinotasikan dengan 1) dan 'perokok yang tidak menderita kanker paru-paru' (bisa dinotasikan dengan 0).

Untuk lebih jelasnya, sekarang misalkan \(Y_1, Y_2, …,Y_N\) adalah data populasi untuk suatu variabel kualitatif yang terdiri dari dua kategori, katakanlah kategori-g dan bukan kategori-g. Dalam populasi berukuran N tersebut, masing-masing Y termasuk dalam salah satu dari kategori-g atau bukan kategori-g. Frekuensi nisbi atau proporsi unsur dari kategori-g dalam populasi data tersebut adalah \(P_g = f_g/N\), di mana \(f_g\) adalah jumlah populasi yang berkategori-g.

Untuk tujuan kemudahan, dalam kasus ini kategori hanya terbagi menjadi dua saja (dalam kenyataannya bisa lebih dari dua kategori), seperti sukses-gagal, benar-salah, merah-bukan merah, atau partai MCK-bukan partai MCK (seperti percobaan Bernoulli), sehingga secara teori bila Y = banyaknya yang ‘sukses’ dari n pengamatan, maka p(y), yaitu peluang Y = y, akan mengikuti distribusi Binomial. Diasumsikan sampel berukuran besar (n cukup besar) sehingga asumsi pendekatan normal dapat dilakukan untuk pendugaan interval dari P.

Pendugaan Proporsi Populasi, \(P\) atau \(π\)

Misalkan \(y_i\) bernilai 0 (tidak berciri tertentu) atau 1 (berciri tertentu) dan \(a\) menotasikan banyaknya unit dalam sampel yang memiliki karakteristik tertentu tersebut (misalnya banyaknya perokok yang menderita kanker paru-paru), maka proporsi unit berciri tertentu tersebut di dalam sampel dengan ukuran n unit yang diambil dari N unit secara SRS-WOR adalah:

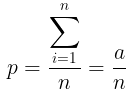
Proporsi sampel p merupakan perkiraan untuk proporsi populasi P atau π, dengan variansnya adalah:

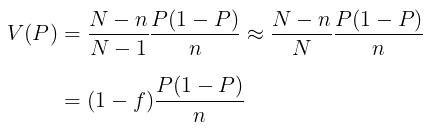
Perkiraan dari varians di atas diberikan oleh:

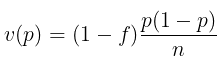
dan perkiraan standard error-nya yaitu:

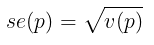
Dengan asumsi bahwa sampel yang dipunyai adalah sampel dengan ukuran yang cukup besar, lebih besari dari 30 (ada yang menyarankan lebih besar dari 50), maka pendugaan interval untuk P dengan tingkat keyakinan \((1-α)\%\) adalah sebagai berikut:

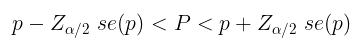
Pendugaan Total Populasi yang Berciri Tertentu

Selain proporsi/persentase populasi, yang biasa dilakukan juga adalah menduga total nilai suatu karakteristik tertentu dalam populasi berdasarkan sampel (A), yaitu dengan rumus sebagai berikut:

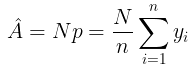
yang merupakan perkiraan dari A dengan variansnya adalah:

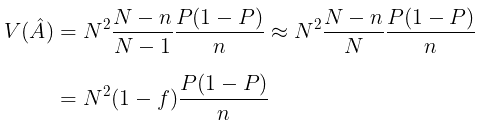
Perkiraan variannya diberikan oleh:

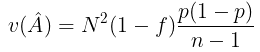
dan perkiraan standard error-nya yaitu:

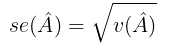
Dengan asumsi bahwa sampel yang dipunyai adalah sampel dengan ukuran yang cukup besar, lebih besari dari 30 (ada yang menyarankan lebih besar dari 50), maka pendugaan interval untuk A dengan tingkat keyakinan (1-α)% adalah sebagai berikut:

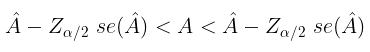
Dalam pembuatan pendugaan interval, nilai Z yang biasa digunakan adalah nilai Z yang berdasarkan tingkat keyakinan (confidence level) 90%, 95% dan 99%. Dengan demikian, nilai Z yang biasa dipakai adalah: 1,64 atau 1,65; 1,96; dan 2,58 secara berturut-turut.

Contoh 1:

Dari populasi 300 perguruan tinggi diambil sebuah sampel acak sederhana tanpa pengembalian (SRS-WOR) sebanyak 60 perguruan tinggi. Dari sampel tersebut, 36 perguruan tinggi di antaranya menyatakan setuju dengan rencana pengembangan kurikulum terbaru, sedangkan 24 perguruan tinggi menolak rencana tersebut. Berdasarkan informasi tersebut, buatlah perkiraan persentase banyaknya perguruan tinggi dalam populasi yang menyatakan setuju akan rencana pengembangan kurikulum terbaru beserta standard errornya dan pendugaan interval dengan tingkat keyakinan 95%!

Pembahasan:

Diketahui bahwa N = 300; n = 60; a = 36. Maka perkiraan persentase banyaknya perguruan tinggi yang setuju dengan rencana pengembangan kurikulum terbaru adalah p, yaitu:

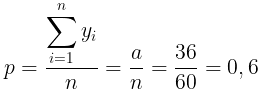
dengan varians dan standar error:

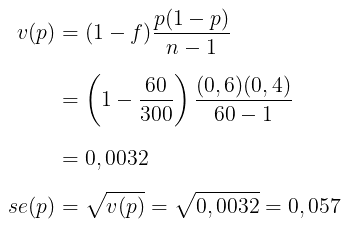
Perkiraan banyaknya perguruan tinggi yang setuju adalah:

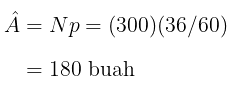
dengan varians dan standar error dari perkiraan banyaknya perguruan tinggi yang setuju adalah:

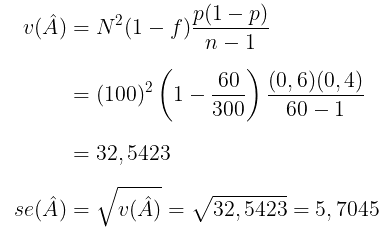
Dengan demikian, pendugaan interval banyaknya perguruan tinggi yang setuju dengan tingkat keyakinan 95% adalah sebagai berikut:

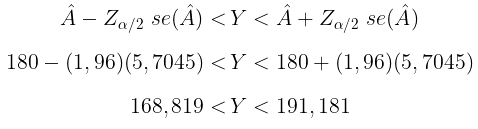
Jadi, dengan tingkat keyakinan 95% dapat disimpulkan bahwa banyaknya perguruan tinggi yang setuju dengan rencana pengembangan kurikulum terbaru akan berada dalam rentang 169 sampai 192 perguruan tinggi.

Sumber:

Asra, Abuzar & Achmad Prasetyo. 2015. Pengambilan Sampel dalam Penelitian Survei. PT RajaGrafindo Persada: Jakarta.