MPC I   »   Simple Random Sampling   ›  Estimasi Rata-rata dan Total Populasi dalam SRS WR

Sampling

Estimasi Rata-rata dan Total Populasi dalam SRS WR

Setelah sampel diperoleh dengan SRS-WR, langkah berikutnya adalah melakukan pendugaan untuk memperoleh parameter atau karakteristik populasi. Pada artikel ini, akan dibahas pendugaan rata-rata dan total populasi dengan SRS WR.

---

Kita telah membahas pendugaan rata-rata dan total populasi dengan SRS tanpa pengembalian (without replacement) pada artikel sebelumnya. Sekarang kita lanjutkan untuk pendugaan rata-rata dan total populasi pada SRS dengan pengembalian (with replacement).

Pendugaan Rata-rata Populasi, μ dan \(\overline{Y}\)

Misalkan terdapat populasi dengan nilai-nilainya yaitu \( Y_1, Y_2, \cdots Y_N \). Kemudian dilakukan penarikan sampel secara acak sederhana dengan pengembalian (SRS WR), sehingga diperoleh sampel yang mengandung nilai \(y_1, y_2,…,y_n\). Statistik rata-rata dan varians yang diperoleh berdasarkan data sampel adalah nilai penduga bagi rata-rata (μ) dan varians populasinya (σ).

Dengan demikian, penduga tak bias (unbiased estimator) bagi rata-rata populasi (μ) adalah rata-rata sampel \( (\overline{y}) \), dengan rumus sebagai berikut:

dengan variansnya adalah

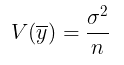
Kemudian, karena \(\sigma^2\) biasanya tidak diketahui, maka perkiraan varians standard error-nya diberikan oleh:

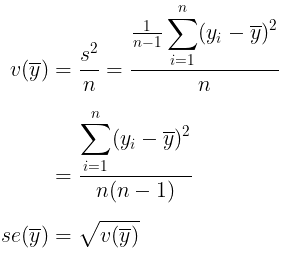
Dengan demikian, tingkat keyakinan (confidence interval) (1-α)% untuk μ adalah:

1. jika populasi normal dan \(\sigma^2\) diketahui,

2. Jika populasi normal dan \(\sigma^2\) tidak diketahui, diperkirakan dengan \(s^2\),

3. jika diasumsikan bentuk distribusi populasi tidak diketahui, tetapi \(\sigma^2\) diketahui dan n mendekati tak berhingga (biasanya digunakan patokan lebih atau sama dengan 30, atau ada juga yang berpendapat lebih atau sama dengan 50),

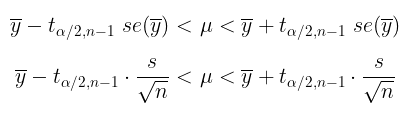
Pendugaan Total Nilai Populasi \(\hat{Y}\)

Selain rata-rata populasi, yang biasa dilakukan juga adalah menduga total nilai suatu karakteristik tertentu dalam populasi berdasarkan sampel, yaitu dengan rumus sebagai beriku:

dengan variansnya adalah:

Adapun perkiraan varians dan standard error-nya (karena \(\sigma^2\) biasanya tidak diketahui) adalah:

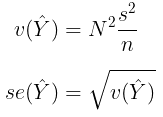
Dengan demikian, tingkat keyakinan (confidence interval) (1-α)% untuk Y adalah:

1. jika populasi normal dan \(\sigma^2\) diketahui,

2. jika populasi normal dan \(\sigma^2\) tidak diketahui, diperkirakan dengan \(s^2\),

3. jika diasumsikan bentuk distribusi populasi tidak diketahui, tetapi \(\sigma^2\) diketahui dan n mendekati tak berhingga (biasanya digunakan patokan lebih atau sama dengan 30, atau ada juga yang berpendapat lebih atau sama dengan 50),

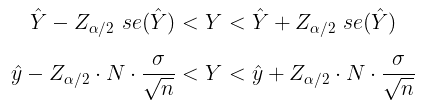
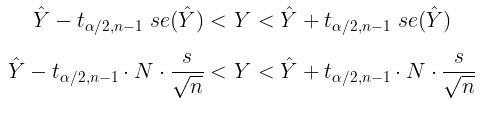
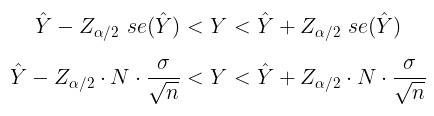
Contoh 1:

Sebuah sampel acak/random sederhana tanpa pengembalian (PSAS-DP) (SRS-WR) sebanyak 15 rumah tangga dipilih dari 120 rumah tangga di sebuah wilayah. Kemudian dicatat jumlah anggota rumah tangga masing-masing rumah tangga (y) dan datanya adalah sebagai berikut:

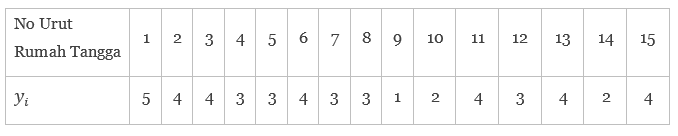
Perkirakan total penduduk yang ada di wilayah tersebut dalam sebuah confidence interval 95%! Diasumsikan bahwa sebaran banyaknya anggota rumah tangga mengikuti sebaran Normal.

Pembahasan:

Diketahui bahwa N = 120; n = 5. Dengan demikian, perkiraan rata-rata anggota rumah tangga per rumah tangga adalah:

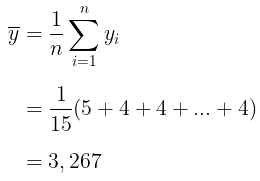
Jadi, rata-rata ada sekitar 3,3 orang per rumah tangga. Selanjutnya, untuk menentukan perkiraan varians dari rata-rata sampel kita hitung nilai \(s^2\) terlebih dahulu:

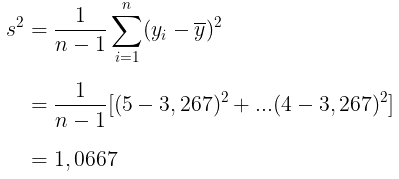
Jadi, perkiraan varians dari rata-rata sampel adalah:

Selanjutnya, perkiraan penduduk di wilayah tersebut adalah:

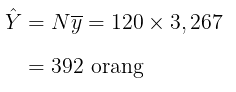
dengan perkiraan varians dan standard error dari perkiraan total penduduk di wilayah tersebut adalah:

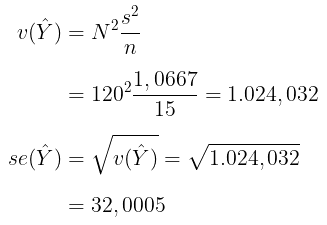
Dengan demikian, pendugaan interval total penduduk di wilayah tersebut dengan tingkat keyakinan 95% adalah sebagai berikut:

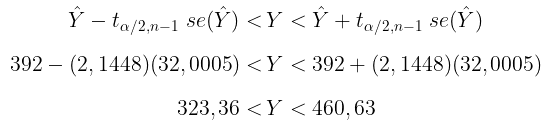
Dengan kata lain, pendugaan interval untuk total penduduk di wilayah tersebut dengan tingkat keyakinan 95% adalah 323 jiwa < Y < 461 jiwa.

Sumber:

Asra, Abuzar & Achmad Prasetyo. 2015. Pengambilan Sampel dalam Penelitian Survei. PT RajaGrafindo Persada: Jakarta.