www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
METODE PENARIKAN CONTOH 1
Metode Penarikan Contoh 1
MPC I » Stratified Random Sampling › Pengalokasian Sampel ke Setiap Strata dalam Stratified Random Sampling
Sampling
Pengalokasian Sampel ke Setiap Strata dalam Stratified Random Sampling
Terdapat minimal lima cara mengalokasikan sampel sebesar n ke setiap strata, antara lain alokasi sembarang/subjektif; alokasi sama (equal allocation); alokasi proporsional (proportional allocation); alokasi Neyman; dan alokasi Optimum.
Seperti telah dijelaskan sebelumnya bahwa stratified random sampling atau pengambilan sampel acak berstrata adalah teknik pengambilan sampel dengan terlebih dahulu membuat populasi menjadi beberapa subpopulasi (lapisan, strata) dan kemudian mengambil sampel dari setiap subpopulasi tersebut.
Bila sudah ditentukan banyaknya lapisan yang akan digunakan, katakanlah sebanyak L strata (lapisan) dan besarnya sampel yang akan diamati yakni sebesar n sampel, maka tahap selanjutnya adalah bagaimana mengalokasikan n sampel tersebut ke setiap lapisan, yaitu berapa besarnya \(n_h\) untuk setiap \(h = 1, 2, …,L\) dengan syarat \( \displaystyle \sum_{h=1}^{L} n_h =n\).
Terdapat minimal lima cara mengalokasikan sampel sebesar n ke setiap lapisan, antara lain alokasi sembarang/subjektif (random/subjective allocation); alokasi sama (equal allocation); alokasi proporsional (proportional allocation); alokasi Neyman; dan alokasi Optimum. Kita akan membahas kelima cara pengalokasian tersebut berikut ini.
Alokasi Sembarang/Subjektif (Random/Subjective Allocation)
Sesuai dengan namanya yakni alokasi sembarang atau subjektif, maka cara pengalokasian ini terserah kepada selera si peneliti. Misalkan suatu populasi berukuran N dibagi-bagi ke dalam L strata, sedemikian rupa sehingga

dan total sampel berukuran n dialokasikan ke setiap strata secara sembarang atau berdasarkan pertimbangan subjektif peneliti sedemikian rupa sehingga
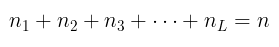
Alokasi Sama (Equal Allocation)
Dengan cara pengalokasian ini, maka besarnya sampel pada setiap lapisan atau strata adalah sama besar, tanpa memerhatikan situasi lapisan. Misalkan suatu populasi yang berukuran N dibagi-bagi ke dalam L strata sedemikian sehingga
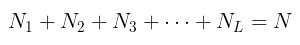
dan total sampel berukuran n dialokasikan ke setiap strata secara sama, yaitu:
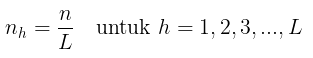
Alokasi Proporsional (Proportional Allocation)
Dalam alokasi proporsional atau sebanding, besarnya sampel pada setiap lapisan tergantung pada banyaknya unit dalam lapisan tersebut. Untuk lapisan yang besar, dalam pengertian mempunyai banyak unit sampling, akan diambil sampel lebih banyak dibandingkan lapisan yang kecil. Pada umumnya, alokasi proporsional digunakan apabila rata-rata antara strata yang satu dengan yang lainnya berbeda sekali.
Keuntungan dari alokasi sebanding adalah kepraktisan pengolahan (tabulasi) hasil survei. Hal ini disebabkan karena prosedur ini akan menghasilkan penduga yang tertimbang secara otomatis (self-weighted estimator).
Dengan cara pengalokasian ini, maka \(n_h\) ditentukan sebagai berikut:
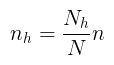
di mana:
\(N_h =\) banyaknya unit pada lapisan ke-h
\(N =\) banyaknya unit pada seluruh lapisan \(= \displaystyle \sum_{h=1}^L N_h =N\)
\(n_h =\) banyaknya sampel pada lapisan ke-h (diambil dari \(N_h\) unit)
\(n =\) banyaknya sampel pada seluruh lapisan \(= \displaystyle \sum_{h=1}^L n_h\)
Contoh 1:
Misalkan ada lima strata dengan banyaknya unit di setiap strata/lapisan adalah sebagai berikut: 10, 10, 20, 30, 30 (N = 100). Bila akan diamati hanya 20 unit (n = 20), maka:

Dengan demikian, seluruhnya adalah n = 20.
Alokasi Neyman (Neyman Allocation)
Besarnya sampel di setiap lapisan tidak hanya tergantung pada besarnya lapisan, tetapi juga pada tingkat homogenitas atau heterogenitas dari ciri unit-unit pada lapisan tersebut.
Dalam bentuk rumus, alokasi Neyman dapat dituliskan sebagai berikut:
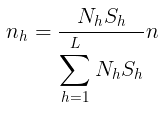
di mana \(S_h\) adalah deviasi standar lapisan ke-h.
Dengan bertambahnya heterogenitas dalam suatu lapisan (yang lain tetap), maka akan bertambah banyak pula sampel yang harus diambil dari lapisan tersebut. Alokasi ini dilakukan untuk memperkecil standard error dari perkiraan.
Alokasi Optimum (Optimum Allocation)
Bila ada perbedaan yang sangat besar dalam biaya wawancara per unit dan keragaman populasi antar lapisan, total biaya survei pada suatu tingkat ketelitian tertentu yang dikehendaki dapat diminimumkan dengan memperhitungkan kedua faktor di atas, yaitu variasi dan biaya per unit.
Dengan demikian, nama alokasi ini adalah alokasi optimum, yaitu mengoptimumkan total biaya yang tersedia dengan memerhatikan keragaman di dalam setiap subpopulasi serta biaya per unit di setiap subpopulasi.
Fungsi linier dari biaya dalam sampling berstrata adalah:

di mana: C= total biaya, Co = biaya tetap dan Ch = biaya per wawancara per unit pada lapisan ke-h.
Apabila dikaitkan dengan varians, maka ada dua kondisi yang harus dipertimbangkan, yaitu: (i) meminimumkan varians dengan biaya tetap atau (ii) meminimumkan biaya dengan varians tetap. Namun, keduanya sama-sama meminimalkan varians penduga yang dihasilkan. Misalkan:
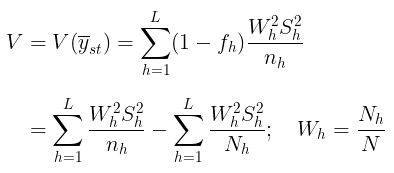
Untuk menentukan nilai optimum dari n, kita pertimbangkan fungsi:
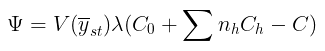
di λ adalah konstanta, yang merupakan sebuah Lagrange Multiplier, yang tidak diketahui nilainya.
Kemudian \(n_h\) diperoleh dengan meminimumkan Ψ, yaitu dengan mendiferensiasi parsial Ψ terhadap \(n_h\) dan menyamakan hasilnya dengan 0 (nol). Dengan demikian, akan diperoleh:
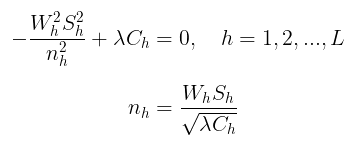
Dengan menjumlahkan seluruh strata kita peroleh:
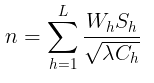
Dengan demikian, alokasi sampel ke lapisan h, adalah (karena Wh = Nh/N dan λ adalah suatu bilangan tetap):
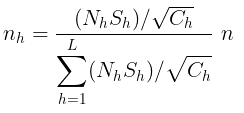
Dengan kata lain, (i) total sampel yang berukuran n ketika biaya tetap adalah:
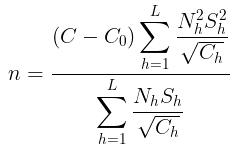
dan (ii) total sampel yang berukuran n ketika varians tetap adalah:
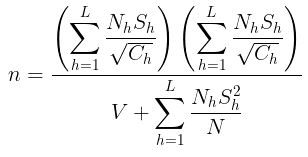
Contoh 2:
Ada empat kelompok perusahaan industri pengolahan di suatu kabupaten yakni perusahaan industri besar, sedang, kecil dan rumah tangga. Akan diamati sebanyak 34 perusahaan industri. Diberikan banyaknya perusahaan, tingkat keragaman ciri (misalnya banyak buruh) dan biaya wawancara/pengamatan per perusahaan pada tabel di bawah ini.

Bagaimana alokasi sampel sebanyak 34 perusahaan tersebut ke keempat tipe industri yang ada?
Pembahasan:
- Bila kita abaikan perbedaan Ch, yaitu kita anggap Ch = C (sama untuk seluruh lapisan), maka cukup kita gunakan Neyman Allocation:
- Bila kita perhatikan adanya perbedaan biaya pengamatan per unit antara lapisan, maka alokasi sampel secara optimum, adalah sebagai berikut:
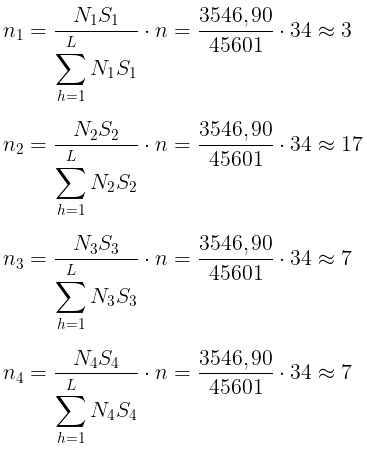
Total sampel = 34 seperti yang dikehendaki dengan alokasi seperti di atas.

Dengan cara yang sama diperoleh:

Total sampel = 34 seperti yang ingin dicapai.
Sumber:
Asra, Abuzar & Achmad Prasetyo. 2015. Pengambilan Sampel dalam Penelitian Survei. PT RajaGrafindo Persada: Jakarta.
Artikel Terkait
Belajarlah mengalah sampai tak seorangpun yang bisa mengalahkanmu. Belajarlah merendah sampai tak seorangpun yang bisa merendahkanmu.
Gobind Vashdev
