Analisis Regresi   »   Regresi Linear Sederhana   ›  Estimasi Model Regresi dengan Metode OLS

Analisis Regresi

Estimasi Model Regresi dengan Metode OLS

Metode OLS (ordinary least square) digunakan untuk mengestimasi nilai koefisien regresi sedemikian rupa sehingga meminimalkan kuadrat residual.

Oleh Tju Ji Long · Statistisi

Dalam analisis regresi, hubungan antara variabel tak bebas \(Y\) dan satu variabel bebas \(X\) dapat dinyatakan dalam persamaan model berikut:

\[ Y_i = β_0 + β_1 X_i + ε_i \]

Sebagai contoh, misalkan kita mempunyai data total penjualan yang dinyatakan dengan Y dan biaya iklan yang dinyatakan dengan X. Plot pada Gambar 1 melukiskan hubungan antara biaya yang dikeluarkan untuk iklan (\(X\)) dan total penjualan (\(Y\)).

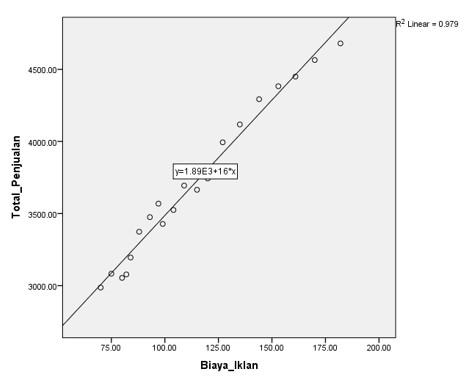
Gambar 1. Plot antara total penjualan dan biaya iklan.

Pada persamaan model regresi yang diberikan di atas, idealnya kita perlu mencari nilai \(β_0\) dan \(β_1\) sedemikian sehingga garis \(Y=β_0+β_1 X\) terletak pada semua observasi. Namun, dalam kenyataannya, dapat dikatakan suatu kemustahilan garis regresi yang didapat berada tepat pada semua observasi.

Berdasarkan kenyataan tersebut, upaya terbaik yang dapat dilakukan yaitu dengan mencari nilai \(β_0\) dan \(β_1\) sedemikian sehingga penyimpangan atau deviasi antara garis \(Y=β_0+β_1 X\) dengan titik-titik observasi atau pengamatan adalah sekecil mungkin. Dengan kata lain, nilai error yang dilambangkan dengan \(ε_i\) dalam persamaan model regresi diminimalkan.

Secara umum, untuk memperoleh taksiran nilai bagi \(β_0\) dan \(β_1\) atau \(\hat{β}_0\) dan \(\hat{β}_1\) (ingat, tanda topi di atas melambangkan nilai taksiran) yang meminimumkan error, kita bisa menggunakan metode kuadrat terkecil biasa (Ordinary Least Square – OLS method) atau metode maksimum likehood (maximum likelihoood estimator - MLE method).

Metode Kuadrat Terkecil (Ordinary Least Square)

Parameter yang tidak diketahui \((β_0,β_1,…,β_k)\) dalam model regresi linear biasanya diestimasi menggunakan metode kuadrat terkecil (least squares method).

Pada prinsipnya, metode kuadrat terkecil ini digunakan untuk memperkirakan semua nilai koefisien regresi \(β\) (\(β_0\) dan \(β_1\) jika regresi linier sederhana dan \(β_0, β_1\) hingga \(β_k\) jika regresi linier berganda) sedemikian rupa sehingga meminimalkan kuadrat residual \( \left(∑_\limits{i=1}^n ε_i^2 \right)\).

Misalkan \(S\) adalah kuadrat residual, maka dapat dituliskan sebagai berikut:

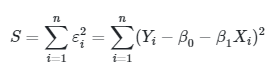(1)

Nilai \(\hat{β}_0\) dan \(\hat{β}_1\) yang diperoleh merupakan nilai taksiran atau nilai dugaan (estimator/penduga) bagi \(β_0\) dan \(β_1\) yang mana jika nilai-nilai ini dimasukkan ke dalam persamaan regresi linier sederhana maka akan diperoleh kuadrat residual yang minimum atau yang paling kecil. Untuk menjelaskan bagaimana ini bisa terjadi, kita dapat menggunakan konsep turunan yang kita pelajari dalam Kalkulus 1.

Kita dapat menentukan \(\hat{β}_0\) dan \(\hat{β}_1\) dengan cara mendiferensiasi \(S\) secara parsial (differentiating partially) terhadap masing-masing \(β_0\) dan \(β_1\) dan kemudian menyamakan hasil pendiferensian itu dengan nol.

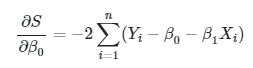	(2)
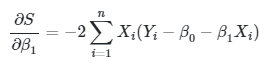	(3)

Dengan menyamakan hasil pendiferensialan dengan nilai nol, kita peroleh:

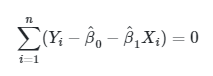	(4)
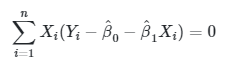	(5)

Perhatikan bahwa kita mengganti \( β_0 \) dengan \( \hat{β}_0 \) dan \( β_1 \) dengan \( \hat{β}_1 \) ketika menyamakan hasil pendiferesialan dengan nol. Mengapa?

Dari persamaan (4), diperoleh:

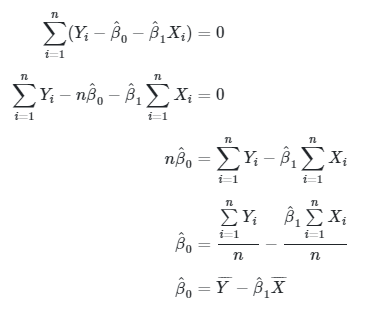
Dengan demikian, taksiran bagi \( β_0 \) yaitu

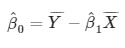(6)

Selanjutnya, dari persamaan (5) diperoleh:

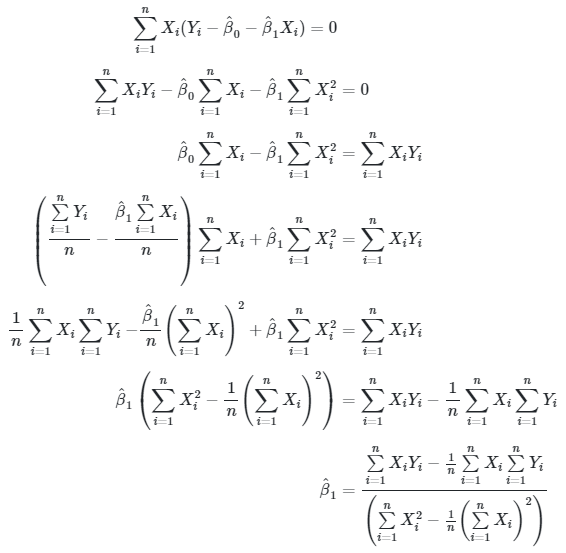
Dengan demikian, taksiran bagi \( β_1 \), yaitu:

(7)

Dengan sedikit modifikasi, kita juga dapat menyatakan taksiran bagi \( β_1 \) menjadi:

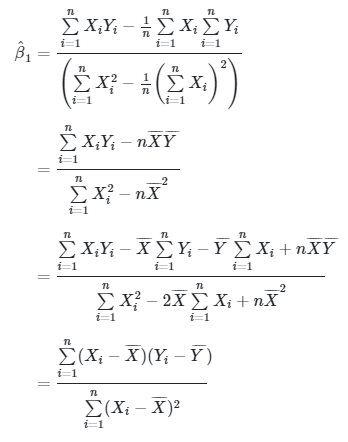
Jadi, \( \hat{β}_1 \) dapat juga kita nyatakan dengan:

(8)

Sebelum mengakhiri artikel ini, ada satu pertanyaan yang sering muncul mengenai estimasi titik parameter model regresi menggunakan metode OLS: Mengapa dalam metode OLS digunakan kuadrat residual \(∑_\limits{i=1}^n ε_i^2 \) dan bukan \(∑_\limits{i=1}^n ε_i \) saja?

Untuk menjawab pertanyaan tersebut, perhatikan gambar berikut ini:

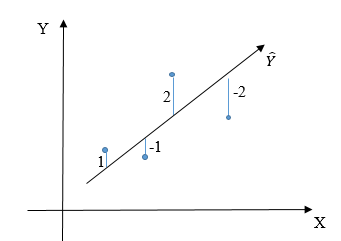
Dari gambar di atas, terlihat bahwa garis regresinya sudah terlihat bagus yang mana \(∑_\limits{i=1}^n ε_i = 0 \) padahal tidak ada satupun data yang berada di garis regresi. Ini berarti garis regresi atau model regresi yang diperoleh sebenarnya belum cukup baik. Itulah kenapa digunakan \(∑_\limits{i=1}^n ε_i^2 \) karena dapat memberikan gambaran yang lebih baik.

Demikian penjelasan mengenai metode kuadrat terkecil biasa (ordinary least square method) untuk memperkirakan nilai koefisien parameter model regresi, yakni \(\hat{β}_0\) dan \(\hat{β}_1\).