Analisis Regresi   »   Asumsi Homoskedastisitas   ›  Asumsi Homoskedastisitas

Analisis Regresi

Asumsi Homoskedastisitas

Salah satu asumsi penting dalam model regresi linear klasik ialah bahwa error \((ε_i)\) mempunyai varian yang sama. Ini disebut asumsi homoskedastisitas.

Salah satu metode statistik yang paling sering digunakan dan diminati oleh banyak peneliti adalah analisis regresi baik itu regresi sederhana (simple regression) maupun regresi berganda (multiple regression).

Salah satu asumsi yang harus dipenuhi ketika menggunakan regresi linier berganda dengan metode OLS (Ordinary Least Square) agar estimasi parameter model bersifat BLUE (Best Linear Unbiased Estimator) adalah homoskedastisitas, yakni semua error mempunyai varians sama atau konstan.

Secara harfiah, homo artinya sama dan skedastisitas artinya penyebaran, sehingga homoskedastisitas berarti sama penyebaran atau sama variannya.

Asumsi homoskedastisitas ini pada intinya ingin mengatakan bahwa varian dari setiap error \((ε_i)\) untuk variabel-variabel bebas yang diketahui merupakan suatu bilangan konstan dengan simbol \(σ^2\). Dalam hal ini bisa dituliskan sebagai:

\[ Var(ε_i) = E(ε_i^2) = σ^2; \quad i = 1,2,...,n \]

Ilustrasi dari asumsi homoskedastisitas dapat ditunjukkan seperti pada Gambar 1 berikut:

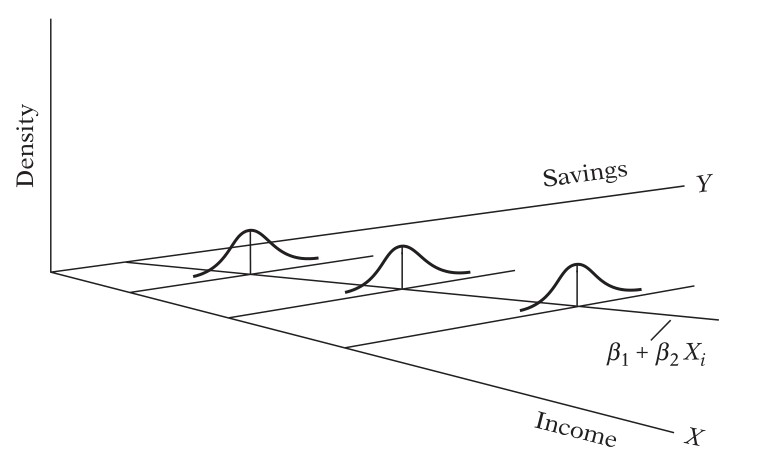
Gambar 1. Kesalahan pengganggu (error) yang homoskedastis

Gambar 1 di atas menunjukkan bahwa varian \(Y_i\) atau varian \(ε_i\) dengan syarat variabel bebas \(X = X_i\), akan tetap sama untuk nilai variabel \(X\) yang berlainan. Perhatikan bahwa untuk \(X\) tertentu, katakanlah \(X = X_i\) akan terjadi beberapa nilai \(Y\). Jadi, untuk nilai konstan \(X_i\), nilai \(Y\) bervariasi. Peubah \(Y\) mempunyai distribusi dan varian, dalam hal ini varian \(Y_i\) sama dengan varian \(ε_i\).

Misalkan ada 5 orang diteliti, masing-masing mempunyai pendapatan (income) yang sama, yaitu Rp1000.000,- per bulan (X = 1000). Akan tetapi, tabungan (saving) dari kelima orang ini berbeda-beda, katakanlah yang pertama Rp80.000,- (Y = Y1), yang kedua Rp75.000,- ( Y = Y2), ketiga Rp60.000,- (Y = Y3), keempat Rp85.000,- (Y = Y4) dan kelima Rp90.000,- ( Y = Y5).

Adapun rata-rata \(Y\) dengan syarat bahwa \(X = 1000\) dapat dituliskan sebagai berikut:

\begin{aligned} E(Y|X=1000) &= \frac{1}{n} \sum_{i=1}^n Y_i \\[8pt] &= \frac{1}{5} (80 + 75 + 60 + 85 + 90) \\[8pt] &= 78 \end{aligned}

Jadi, rata-rata tabungan, dengan syarat pendapatan sebesar Rp1000.000,- adalah Rp78 ribu.

Perhatikan bahwa untuk setiap kelompok pendapatan tertentu, tabungan akan berbeda-beda, yakni:

Pendapatan \(X_1\), tabungannya adalah \(Y_{11}, Y_{12},…,Y_{1n}\)

Pendapatan \(X_2\), tabungannya adalah \(Y_{21}, Y_{22},…,Y_{2n}\)

Pendapatan \(X_3\), tabungannya adalah \(Y_{31}, Y_{32},…,Y_{3n}\)

Pendapatan \(X_4\), tabungannya adalah \(Y_{41}, Y_{42},…,Y_{4n}\)

Dalam keadaan yang homoskedastis, varian dari masing-masing \(Y\) adalah sama, yaitu \(Var(Y_i)=Var(ε_i)=σ^2\). Akan tetapi, dalam keadaan heteroskedastis, varian masing-masing \(Y\) tak sama, dengan simbol sebagai berikut:

\[ Var(Y_i)=Var(ε_i)=σ_i^2 \]

Ini berarti bahwa varian \(Y_i\) atau varian \(ε_i\) dengan syarat bahwa \(X = X_i\) adalah tidak sama untuk \(X\) yang berlainan. Perhatikan Gambar 2 berikut ini.

Gambar 2. Kesalahan pengganggu (error) yang heteroskedastis

Perhatikanlah Gambar 2 di atas. Terlihat bahwa distribusi \(Y\) untuk nilai \(X\) tertentu adalah tidak sama dengan distribusi \(Y\) pada nilai \(X\) lain.

Pada Gambar 1 di atas ditunjukkan bahwa kalau pendapatan naik secara rata-rata, tabungan juga naik. Akan tetapi, varian untuk tabungan sama untuk semua tingkatan pendapatan. Sedangkan dalam Gambar 2, varian tabungan meningkat seiring dengan menaiknya pendapatan.

Hal ini bisa dijelaskan bahwa semakin tinggi pendapatan keluarga, secara rata-rata tabungan mereka akan lebih besar daripada tabungan keluarga dengan pendapatan rendah, tetapi juga lebih bervariasi tabungan mereka (sebab varian makin membesar).