Konsekuensi Jika Terjadi Multikolinieritas

Analisis Regresi » Asumsi Multikolinearitas › Konsekuensi Jika Terjadi Multikolinieritas

Analisis Regresi

Konsekuensi Jika Terjadi Multikolinieritas

Pada artikel ini kita akan membahas beberapa akibat atau konsekuensi jika data yang kita miliki terjadi multikolinearitas.

Apabila data yang kita miliki terjadi multikolinearitas sempurna (perfect multicollinierity) maka koefisien regresi berganda tidak dapat diestimasi (mengapa?).

Akan tetapi, jika terjadi multikolinieritas tidak sempurna maka masih memungkinkan untuk dilakukan taksiran terhadap koefisien regresi berganda. Meskipun koefisien regresinya dapat diestimasi, beberapa akibat akan muncul, yakni:

Variansi besar (dari taksiran OLS)
Interval kepercayaan lebar (variansi besar maka standar error juga besar yang berakibat pada interval kepercayaan yang lebar)
Uji-t tidak signifikan. Variabel bebas yang harusnya signifikan bisa menjadi tidak signifikan karena variansi besar akibat kolinierits. Jadi, nilai standard error yang terlalu besar akan meningkatkan peluang \(β\) tidak signifikan.
Uji F signifikan dan \(R^2\) tinggi, tetapi tidak banyak variabel bebas yang signifikan berdasarkan uji-t.
Koefisien regresi bisa mempunyai nilai yang tidak sesuai dengan substansi, misalnya hubungannya seharusnya positif tetapi malah negatif, atau sebaliknya.

Contoh 1:

Misalnya kita mempunyai data konsumsi, pendapatan dan kekayaan seperti tertera pada tabel berikut:

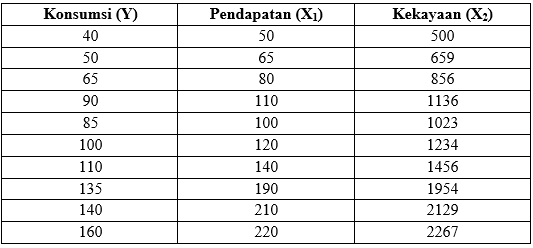
Jika kita perhatikan dengan cermat data pada tabel di atas, kita akan menemukan hubungan antara X1 dan X2 sebagai berikut: X2 = 10X1 + bilangan random. Adanya hubungan ini menunjukkan bahwa data yang kita miliki akan besar kemungkinan terjadi multikolinieritas.

Misalnya kita ingin mengetahui bagaimana pendapatan dan kekayaan mempengaruhi konsumsi, maka model yang diperoleh adalah:

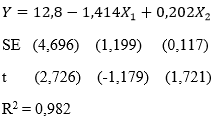
Nilai \(R^2\) yang cukup tinggi yakni sebesar 0,982 menunjukkan bahwa variabel pendapatan dan kekayaan dapat menjelaskan variasi konsumsi sebesar 98,2 persen.

Akan tetapi, berdasarkan uji koefisien secara individu (uji-t) terlihat bahwa tidak ada variabel bebas yang signifikan memengaruhi konsumsi pada tingkat signifikansi 5%. Hal ini disebabkan besarnya nilai standard error akibat terjadinya multikolinieritas.

Selain itu, tanda koefisien regresi pada variabel Pendapatan yang bernilai negatif menunjukkan bahwa semakin tinggi pendapatan maka konsumsinya akan semakin menurun. Interpretasi semacam ini tentu saja bisa menyesatkan. Karena sangatlah tidak mungkin pendapatan yang semakin tinggi akan berakibat pada menurunnya konsumsi.

Hasil yang berbeda akan diperoleh jika kita hanya memasukkan salah satu variabel saja yaitu antara pendapatan atau kekayaan. Perhatikan model yang diperoleh di bawah ini:

Persamaan 1:

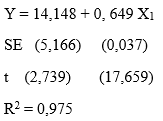
Persamaan 2:

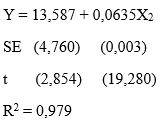
Pada persamaan 1, diperoleh nilai \(R^2\) yang cukup tinggi yakni 0,975 yang mana menunjukkan bahwa model dengan variabel bebas pendapatan dapat menjelaskan 97,5% variasi dari konsumsi. Selain itu, berdasarkan uji-t, koefisien regresinya signifikan pada tingkat signifikansi α = 5%.

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

ANALISIS REGRESI

Analisis Regresi » Asumsi Multikolinearitas › Konsekuensi Jika Terjadi Multikolinieritas

Analisis Regresi