Analisis Regresi   »   Asumsi Autokorelasi   ›  Uji Run untuk Mendeteksi Autokorelasi

Analisis Regresi

Uji Run untuk Mendeteksi Autokorelasi

Uji Run bisa dipakai untuk menentukan apakah residual bersifat acak atau tidak. Jika residual bersifat acak, maka tidak terjadi autokorelasi. Sebaliknya, jika residual bersifat tidak acak maka terjadi autokorelasi.

Uji Run merupakan salah satu uji dalam statistik nonparametrik yang digunakan untuk menentukan apakah data yang kita miliki bersifat acak atau tidak. Dalam kasus untuk mendeteksi autokorelasi, uji ini bisa dipakai untuk menentukan apakah residual yang diperoleh dari model regresi bersifat acak atau tidak.

Jika dari pengujian disimpulkan residualnya bersifat acak maka data yang kita miliki tidak terjadi autokorelasi. Sebaliknya, jika residualnya bersifat tidak acak maka terjadi autokorelasi.

Untuk menjelaskan uji run ini, mari kita tuliskan tanda ( + atau - ) berdasarkan residual yang diperoleh dari regresi antara upah dan produktivitas yang diberikan pada Tabel 1 berikut.

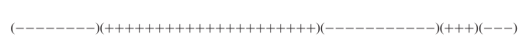
Tabel 1. Residual dari regresi antara upah dan produktivitas tahun 1960 – 2005.

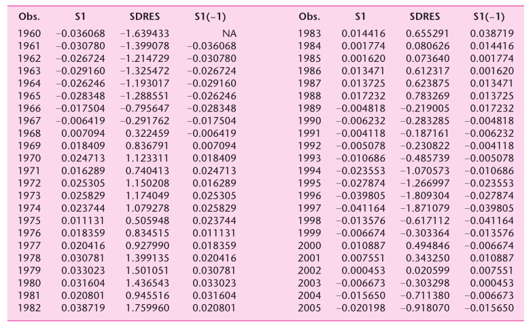
Catatan: S1 = residual dari regresi antara upah-produktivitas dalam model log-linear; S1(-1) = residual lag satu periode dan SDRES = residual terstandarisasi yang diperoleh dari nilai residual dibagi estimasi standar error-nya.

Berdasarkan Tabel 1 di atas, terdapat 8 residual yang bernilai negatif, diikuti oleh 21 residual positif, diikuti oleh 11 residual negatif, kemudian diikuti oleh 3 residual positif dan terakhir diikuti oleh 3 residual negatif untuk total 46 observasi.

Sekarang kita definisikan run sebagai urutan tanpa gangguan dari satu simbol atau atribut. Selanjutnya, kita definisikan panjang run sebagai banyaknya elemen yang ada di dalamnya.

Dengan demikian, dalam rangkaian yang ditunjukkan di atas, terdapat 5 run: yaitu sebuah run yang terdiri dari 8 tanda minus, sebuah run yang terdiri dari 21 tanda positif, sebuah run dengan 11 tanda negatif, sebuah run dengan 3 tanda positif dan terakhir sebuah run dengan 3 tanda negatif.

Dengan mengkaji bagaimana run berperilaku dalam sebuah rangkaian observasi, kita bisa menurunkan sebuah uji keacakan run. Kita akan bertanya begini, “Apakah 5 run dalam data yang mempunyai 46 observasi terlalu sedikit atau terlalu banyak dibandingkan dengan banyaknya run yang diharapkan dalam sebuah rangkaian acak yang terdiri dari 46 observasi?”

Jika terdapat terlalu banyak run, itu berarti dalam contoh kita residualnya berubah tanda terlalu sering, oleh karena itu mengindikasikan autokorelasi negatif. Begitu pula, jika terdapat terlalu sedikit run, itu berarti terjadi autokorelasi positif.

Sekarang misalkan N = total jumlah observasi = N1 + N2; N1 = jumlah simbol + (yakni banyaknya residual yang positif +); N2 = jumlah simbol – (yakni banyaknya residual yang negatif -); R = jumlah run

Kemudian, di bawah hipotesis nol bahwa residual adalah acak, dan dengan mengasumsikan bahwa N1 > 10 dan N2 > 10, jumlah run akan berdistribusi normal dengan rata-rata dan varians

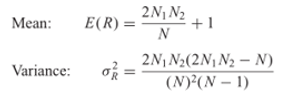
Selain itu, kita peroleh

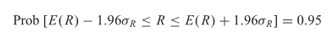
yang artinya peluang 95 persen bahwa interval tersebut akan mencakup R.

Oleh karena itu, kita mempunyai aturan ini: Jangan menolak hipotesis nol dengan tingkat kepercayaan 95% jika R (jumlah run) berada dalam interval kepercayaan; tolak hipotesis nol jika nilai estimasi R berada di luar batas interval tersebut.

Dalam contoh yang diberikan di atas, kita tahu bahwa N1, jumlah plus, adalah 24 dan N2, jumlah minus, adalah 22 dan R = 55. Dengan menggunakan rumus di atas, kita peroleh

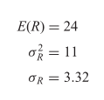
Interval kepercayaan 95% untuk R dalam contoh kita adalah

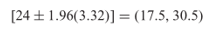
Karena interval ini tidak mencakup 5, maka kita bisa menolak hipotesis nol bahwa residual dalam regresi antara upah dan produktivitas adalah bersifat acak dengan tingkat kepercayaan 95%.

Dengan kata lain, residualnya tak acak sehingga menunjukkan autokorelasi. Sebagai aturan umum, jika terjadi autokorelasi positif maka jumlah run akan sedikit, sedangkan jika autokorelasi negatif, jumlah run akan terlalu banyak.

Jika N1 dan N2 kurang dari 20, kita bisa menggunakan tabel nilai kritis banyaknya run yang diharapkan dalam sebuah rangkaian acak N observasi. Dengan menggunakan tabel ini, kita bisa melihat bahwa residual dalam model regresi antara upah dan produktivitas adalah memang tidak acak; dan residualnya berkorelasi positif.

Sumber:

Gurajarati, Damodar N & Dawn C Porter. Basic Econometrics, 5th ed. New York: McGraw-Hill Companies, Inc.