
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
ANALISIS REGRESI
Analisis Regresi
Regresi Linear Sederhana
Regresi Linear Berganda
Analisis Regresi » Regresi Linear Berganda › Persamaan Regresi Linear Berganda
Analisis Regresi
Persamaan Regresi Linear Berganda
Model regresi yang banyak digunakan adalah regresi linear berganda (multiple regression), di mana terdapat satu variabel tak bebas dan beberapa variabel bebas.
Sejauh ini kita telah membahas mengenai regresi linier sederhana yang bertujuan untuk memodelkan hubungan antara dua variabel. Akan tetapi, dalam kehidupan sesungguhnya, amatlah jarang dijumpai bahwa perubahan suatu variabel tak bebas hanya disebabkan atau berkaitan dengan perubahan yang terjadi dari satu variabel bebas saja.
Dunia, pada kenyataannya, adalah suatu fenomena yang kompleks yang mana tidak hanya dipengaruhi oleh satu faktor melainkan oleh berbagai macam faktor. Dengan kata lain, mengaitkan perubahan suatu fenomena, dalam hal ini satu variabel tak bebas, dengan hanya satu variabel bebas amatlah terlalu bersifat penyederhanaan yang tidak menggambarkan realita.
Berdasarkan kenyataan tersebut, maka model regresi yang banyak digunakan adalah regresi linear berganda (multiple regression), di mana terdapat satu variabel tak bebas dan beberapa variabel bebas.
Sebagai contoh, dalam produksi garmen, rendah tingginya produksi garmen tersebut akan dipengaruhi oleh berbagai faktor, seperti besarnya investasi perusahaan, banyaknya tenaga kerja yang digunakan, jumlah mesin yang tersedia, keterampilan para pekerja, dan besarnya dukungan teknologi. Bila ingin dibuat model yang mengakomodasi seluruh faktor yang memengaruhi tersebut, tentunya tidak dapat digunakan model regresi sederhana.
Dengan regresi linier berganda, ada beberapa hal yang bisa dilakukan yakni:
- Menjelaskan hubungan antara variabel tak bebas dengan variabel bebas
- Berdasarkan hubungan tersebut, kita dapat memperkirakan nilai variabel tak bebas berdasarkan informasi tentang satu (beberapa) variabel bebas;
- Menentukan dampak dari setiap variabel bebas terhadap variabel tak bebas, dengan ‘mengontrol’ variabel bebas lain atau variabel bebas yang lain diasumsikan tidak berubah atau tetap (holding other variables constant). Ini dilakukan dengan melihat besaran koefisien regresi parsial (parsial regression coefficients).
Persamaan Model Regresi Linear Berganda
Model regresi biasanya mencakup lebih dari satu variabel bebas. Model regresi yang digunakan untuk memodelkan hubungan antara satu variabel tak bebas dan beberapa variabel bebas disebut model regresi berganda (multiple regression). Jika terdapat k variabel bebas, model regresi linear berganda dapat dituliskan sebagai:
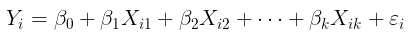
di mana: \( i = 1,2,3,...N \) (banyak observasi populasi); \( β_0, β_1, \dots, β_k \) = koefisien parameter regresi berganda; \(X\) = variabel bebas; \( ε_i \) = kesalahan acak (error term).
Sebagaimana dalam regresi sederhana, nilai koefisien parameter tersebut akan diduga berdasarkan data sampel, sehingga modelnya menjadi:
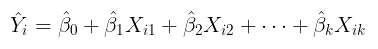
di mana: \( i = 1,2,3,...n \) (banyak observasi sampel); \( \hat{β}_0, \hat{β}_1, \dots, \hat{β}_k \) = taksiran/estimasi koefisien parameter regresi dan \(X\) = variabel bebas.