www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
ANALISIS REGRESI
Analisis Regresi
Regresi Linear Sederhana
Regresi Linear Berganda
Analisis Regresi » Regresi Linear Berganda › Persamaan Regresi Linear Berganda dalam Bentuk Matriks
Analisis Regresi
Persamaan Regresi Linear Berganda dalam Bentuk Matriks
Sama seperti halnya dalam model regresi sederhana, kita juga dapat menyatakan model regresi linear berganda dalam bentuk matriks.
Sama seperti halnya dalam model regresi sederhana, kita juga dapat menyatakan model regresi linear berganda dalam bentuk matriks. Anda mungkin masih ingat bahwa model regresi yang mengandung k peubah bebas dapat dituliskan sebagai berikut:
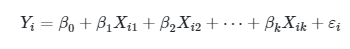
di mana:
\( i = 1,2,3,...N \) (banyak observasi populasi)
\( β_0, β_1, \dots, β_k \) = koefisien parameter regresi
\(X\) = variabel bebas atau independen
\( ε_i \) = kesalahan acak (error term)
Jika diambil n sampel pengamatan, maka terbentuklah sistem persamaan berikut:
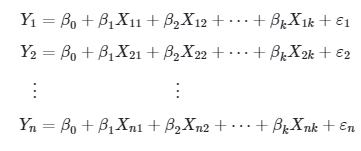
Jika dituliskan dalam lambang matriks, maka sistem persamaan tersebut akan menjadi:
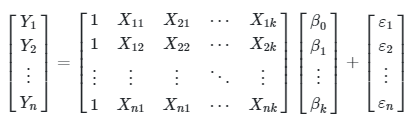
Sekarang, jika dimisalkan
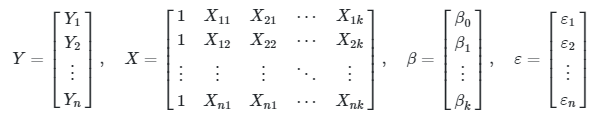
maka sistem persamaan dalam bentuk matriks di atas dapat dituliskan kembali menjadi:
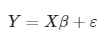
Persamaan terakhir ini merupakan bentuk umum persamaan regresi berganda dalam lambang matriks. Dalam bentuk ini, \(Y\) merupakan vektor peubah tak bebas berukuran n x 1 , \(X\) menyatakan matriks peubah bebas ukuran n x (k+1) , \(β\) vektor parameter ukuran (k+1) x 1 dan \(ε\) vektor galat ukuran n x 1. Ada sebanyak \(k + 1\) parameter yang harus ditaksir dari data, termasuk \(β_0\).
Seperti pada regresi linear sederhana, taksirannya akan ditulis dalam bentuk umum persamaan sebagai berikut:
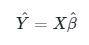
dengan \(\hat{β}\) merupakan taksiran dari \(β\) dan dapat diperoleh dengan rumus
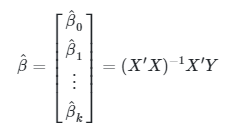
di mana: