RLS dalam Bentuk Matriks

Analisis Regresi » Regresi Linear Sederhana › RLS dalam Bentuk Matriks

Analisis Regresi

RLS dalam Bentuk Matriks

Kita dapat menuliskan persamaan model regresi sederhana dalam bentuk matriks. Hal ini terutama berguna ketika kita bekerja dengan model regresi berganda.

Kita dapat menuliskan persamaan model regresi sederhana dalam bentuk matriks. Hal ini terutama berguna ketika kita bekerja dengan model regresi berganda yang akan kita pelajari pada beberapa artikel berikutnya. Sekarang, perhatikanlah persamaan model regresi sederhana untuk data populasi berikut:

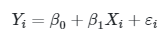
Bila diambil pengamatan sebanyak \(n\), maka persamaan tersebut dapat dituliskan secara lengkap sebagai

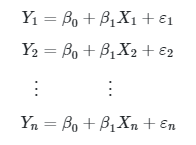
Sistem persamaan di atas dapat dinyatakan dalam bentuk matriks menjadi:

Jika kita misalkan

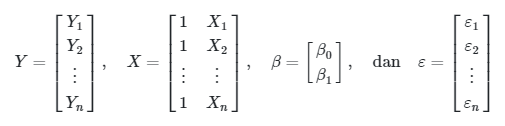
maka persamaan di atas dapat disederhanakan penulisannya menjadi

\[ Y = X β + ε \]

(lambang matriks pada umumnya dinyatakan dengan huruf tebal seperti \(Y,X,β\) dan \(ε\)).

Misalkan terdapat vektor \(\hat{Y}\) yang merupakan taksiran dari \(Y\), dan vektor \(\hat{β}\) yang merupakan taksiran dari \(β\), maka taksiran kuadrat terkecil dari persamaan di atas dapat ditulis sebagai \( \hat{Y} = X \hat{β}\) (Ingat! Galatnya tidak dituliskan karena persamaannya adalah model estimasi).

Contoh 1:

Misalkan terdapat data \(Y\) dengan nilai 2, 1, 4, 5, 3 dan \(X\) dengan nilai 1, 2, 3, 4, 5 serta \(\hat{β}_0 = 1,2 \) dan \(\hat{β}_1 = 0,6 \). Jika ditulis dalam bentuk matriks, maka akan menjadi:

\begin{aligned} Y = \left[ {\begin{array}{cc} 2 \\ 1 \\ 4 \\ 5 \\ 3 \\ \end{array} } \right], \quad X = \left[ {\begin{array}{cc} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \\ \end{array} } \right], \quad \beta = \left[ {\begin{array}{cc} 1,2 \\ 0,6 \end{array} } \right] \\[8pt] \end{aligned}

www.jagostat.com

www.jagostat.com

Website Belajar Matematika & Statistika

Website Belajar Matematika & Statistika

ANALISIS REGRESI

Analisis Regresi » Regresi Linear Sederhana › RLS dalam Bentuk Matriks

Analisis Regresi