
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Bahas Soal Matematika » Integral › Contoh Soal dan Pembahasan Integral Trigonometri Berpangkat
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Contoh Soal dan Pembahasan Integral Trigonometri Berpangkat
Apakah kamu masih mengalami kendala atau mungkin masih bingung cara menyelesaikan integral trigonometri berpangkat? Jika ya, maka ini adalah artikel yang tepat bagimu karena kita akan mengupas secara cukup terperinci cara menyelesaikan integral yang melibatkan fungsi trigonometri berpangkat.
Untuk menyelesaikan integral trigonometri berpangkat kita bisa gunakan beberapa teknik atau metode integral yang sudah dipelajari seperti teknik integral substitusi, teknik integral parsial, dan sebagainya. Di sini kita tidak akan menjelaskan lagi beberapa teknik integral tersebut karena sudah pernah kita bahas di artikel lain.
Sebelum kita masuk ke contoh soal penyelesaian integral trigonometri berpangkat, berikut ini diberikan beberapa rumus atau hasil yang telah diperoleh.


Untuk pembuktian dari masing-masing rumus di atas diberikan di bawah ini.
Untuk integral trigonometri pangkat yang lebih tinggi kita dapat gunakan rumus reduksi berikut ini. Untuk pembuktiannya klik ini: Rumus Reduksi Integral Trigonometri
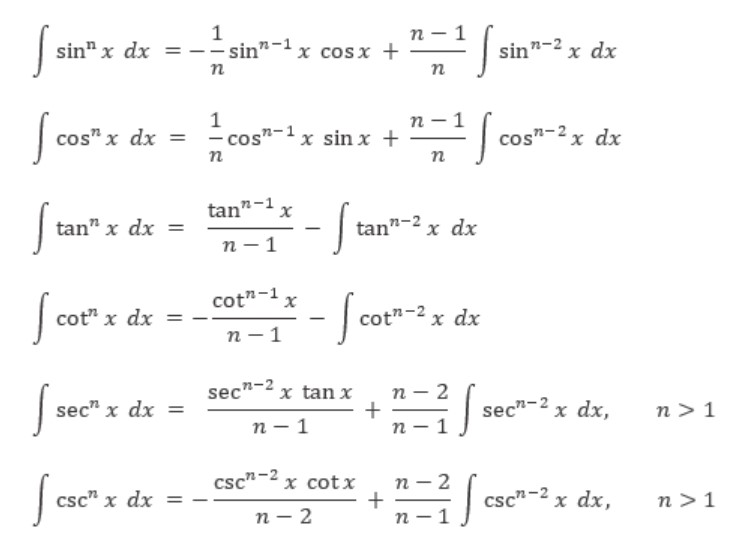
Contoh 1:
Tentukan \( \int \sin^2 x \ dx \).
Pembahasan:
Untuk menyelesaikan soal integral ini kita bisa manfaatkan rumus identitas trigonometri berikut:
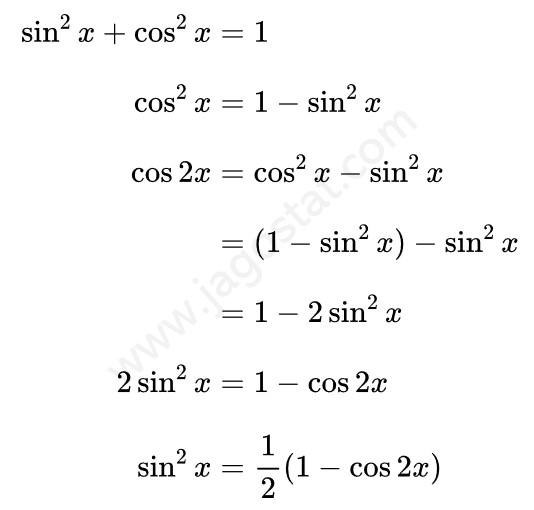
Dengan demikian, integral dari \( \sin^2 x \) adalah…

Contoh 2:
Tentukan \( \int \sin^3 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \sin^3 x \) menjadi \( \sin^2 x \cdot \sin x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \sin^2 x \) menjadi \( 1-\cos^2 x \). Kita peroleh berikut:
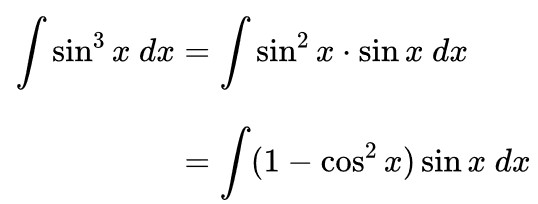
Dari hasil di atas, selesaikan integral menggunakan teknik integral substitusi dengan memisalkan \( u = \cos x \) sehingga diperoleh hasil berikut ini:
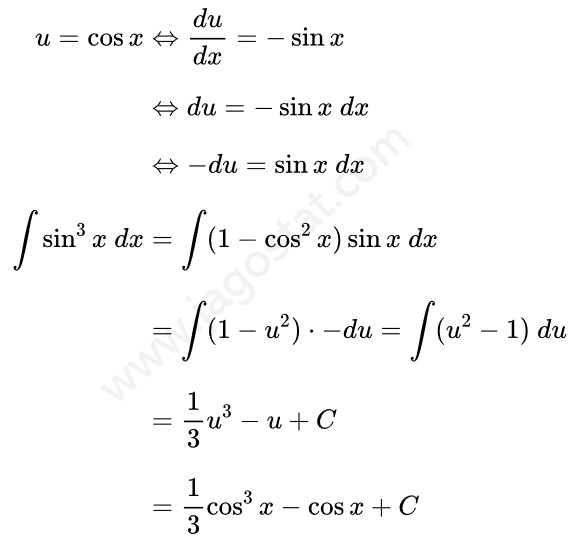
Contoh 3:
Tentukan \( \int \sin^4 x \ dx \).
Pembahasan:
Untuk menyelesaikan soal integral trigonometri ini, kita uraikan dulu fungsi \( \sin^4 x \) menjadi \( (\sin^2 x)^2 \). Kemudian berdasarkan rumus identitas trigonometri, ganti \( \sin^2 x \) menjadi \( \frac{1}{2}(1-\cos 2x) \). Kita peroleh hasil berikut:

Catatan: Berdasarkan rumus identitas trigonometri, \( \cos^2 2x = \frac{1}{2}(1+\cos 4x) \).
Contoh 4:
Tentukan \( \int \sin^5 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \sin^5 x \) menjadi \( (\sin^2 x)^2 \cdot \sin x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \sin^2 x \) menjadi \( 1-\cos^2 x \). Kita peroleh berikut:

Dari hasil di atas, selesaikan integral menggunakan teknik integral substitusi dengan memisalkan \( u = \cos x \) sehingga diperoleh hasil berikut ini:

Contoh 5:
Tentukan \( \int \cos^2 x \ dx \).
Pembahasan:
Untuk menyelesaikan soal integral ini kita akan manfaatkan rumus identitas trigonometri berikut:

Berdasarkan hasil yang diperoleh di atas, penyelesaian integral pada soal yaitu:

Contoh 6:
Tentukan \( \int \cos^3 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \cos^3 x \) menjadi \( \cos^2 x \cdot \cos x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \cos^2 x \) menjadi \( 1-\sin^2 x \). Kita peroleh berikut:

Dari hasil di atas, selesaikan integral menggunakan teknik integral substitusi dengan memisalkan \( u = \sin x \) sehingga diperoleh hasil berikut ini:

Contoh 7:
Tentukan \( \int \cos^4 x \ dx \).
Pembahasan:
Untuk menyelesaikan soal integral trigonometri ini, kita uraikan dulu fungsi \( \cos^4 x \) menjadi \( (\cos^2 x)^2 \). Kemudian berdasarkan rumus identitas trigonometri, ganti \( \cos^2 x \) menjadi \( \frac{1}{2}(\cos 2x+1) \). Kita peroleh hasil berikut:
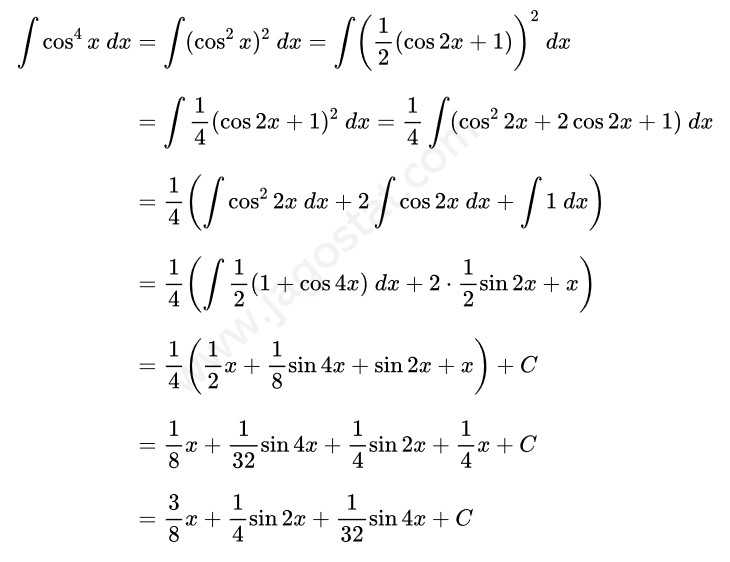
Catatan: Berdasarkan rumus identitas trigonometri, \( \cos^2 2x = \frac{1}{2}(1+\cos 4x) \).
Contoh 8:
Tentukan \( \int \cos^5 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \cos^5 x \) menjadi \( (\cos^2 x)^2 \cdot \cos x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \cos^2 x \) menjadi \( 1-\sin^2 x \). Kita peroleh berikut:

Dari hasil di atas, selesaikan integral menggunakan teknik integral substitusi dengan memisalkan \( u = \sin x \) sehingga diperoleh hasil berikut ini:

Baca juga:
Contoh 9:
Tentukan \( \int \tan^2 x \ dx \).
Pembahasan:
Berdasarkan rumus identitas trigonometri, kita tahu bahwa \( \tan^2 x = \sec^2 x - 1 \) sehingga kita peroleh berikut ini:

Contoh 10:
Tentukan \( \int \tan^3 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \tan^3 x \) menjadi \( \tan^2 x \cdot \tan x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \tan^2 x \) menjadi \( \sec^2 x - 1 \). Kita peroleh berikut:
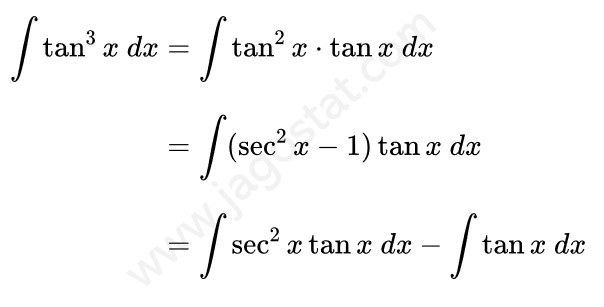
Dari hasil di atas, sekarang kita perlu mencari dua integral. Untuk \( \int \tan x \ dx \) sudah pernah kita bahas di artikel lainnya di mana hasilnya yaitu \( \int \tan x \ dx = \ln|\sec x|+C \) dan untuk integral \( \int \sec^2 x \tan x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \tan x \) sehingga kita peroleh berikut ini:

Contoh 11:
Tentukan \( \int \tan^4 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \tan^4 x \) menjadi \( \tan^2 x \cdot \tan^2 x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \tan^2 x \) menjadi \( \sec^2 x - 1 \). Kita peroleh berikut:

Dari hasil di atas, sekarang kita perlu mencari dua integral. Dalam Contoh 9, \( \int \tan^2 x \ dx = \tan x - x +C \) dan untuk integral \( \int \sec^2 x \tan^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \tan x \) sehingga kita peroleh berikut ini:
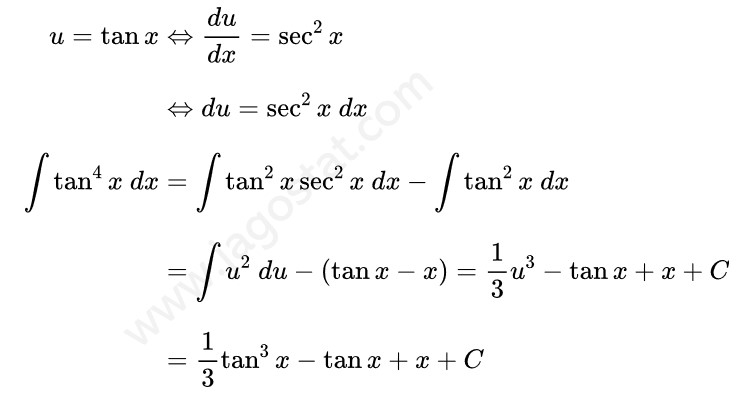
Contoh 12:
Tentukan \( \int \tan^5 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \tan^5 x \) menjadi \( \tan^2 x \cdot \tan^3 x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \tan^2 x \) menjadi \( \sec^2 x - 1 \). Kita peroleh berikut:
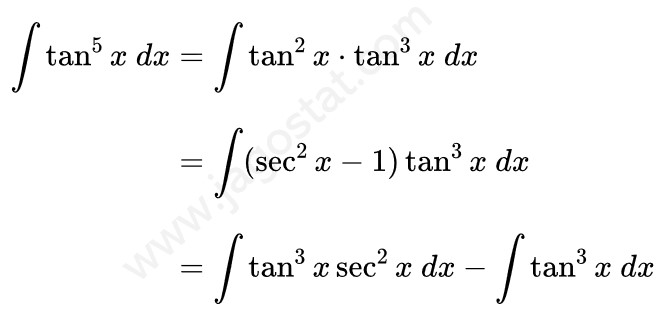
Dari hasil di atas, sekarang kita perlu mencari dua integral. Dalam Contoh 10, \( \int \tan^3 x \ dx = \frac{1}{2}\tan^2 x - \ln|\sec x| +C \) dan untuk integral \( \int \tan^3 x \sec^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \tan x \) sehingga kita peroleh berikut ini:
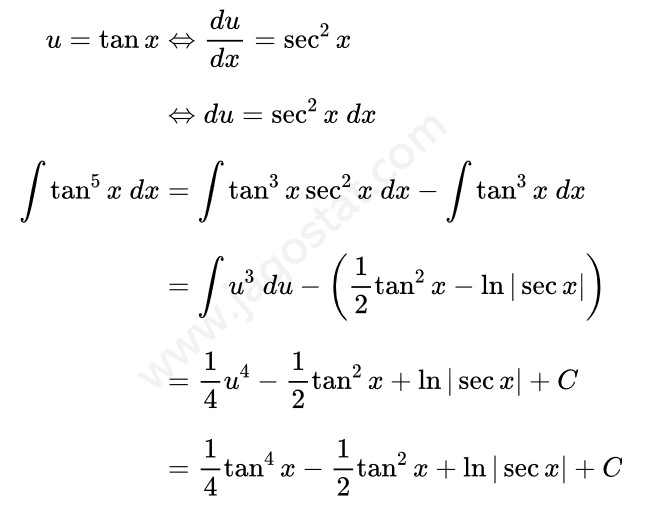
Contoh 13:
Tentukan \( \int \tan^6 x \ dx \).
Pembahasan:
Untuk mengerjakan soal integral ini kita bisa menjabarkan fungsi \( \tan^6 x \) menjadi \( \tan^2 x \cdot \tan^4 x \) terlebih dahulu. Kemudian berdasarkan rumus identitas trigonometri, ganti \( \tan^2 x \) menjadi \( \sec^2 x - 1 \). Kita peroleh berikut:
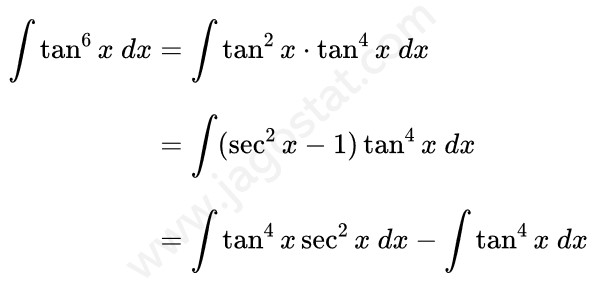
Dari hasil di atas, sekarang kita perlu mencari dua integral. Dalam Contoh 11, \( \int \tan^3 x \ dx = \frac{1}{3}\tan^3 x - \tan x + x + C \) dan untuk integral \( \int \tan^4 x \sec^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \tan x \) sehingga kita peroleh berikut ini:
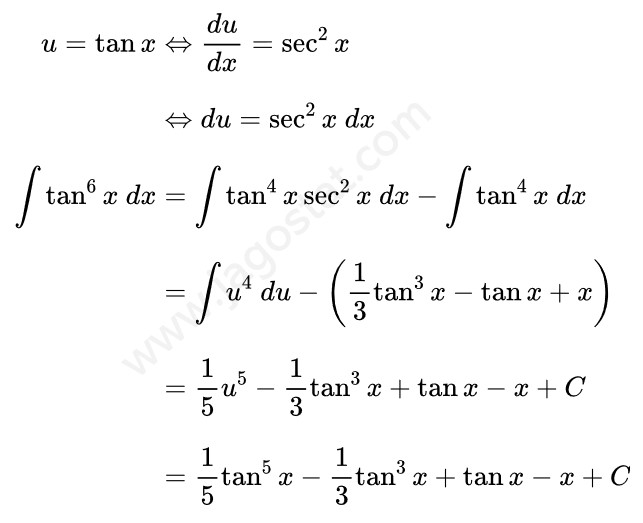
Contoh 14:
Tentukan \( \int \csc^2 x \ dx \).
Pembahasan:
\begin{aligned} \int \csc^2 x \ dx = -\cot x + C \end{aligned}
Contoh 15:
Tentukan \( \int \csc^3 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \csc^3 x \) menjadi \( \csc x \cdot \csc^2 x \). Lalu berdasarkan rumus identitas trigonometri, ganti fungsi \( \csc^2 x \) menjadi \( (1+\cot^2 x) \). Kita peroleh hasil berikut:
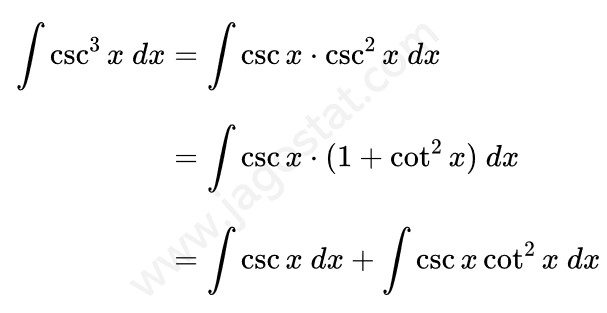
Dari hasil di atas, sekarang kita akan mencari \( \int \csc x \ dx \) dan \( \int \csc x \cot^2 x \ dx \). Kita sudah pernah mencari integral \( \int \csc x \ dx \) di mana hasilnya yaitu \( \int \csc x \ dx = \ln|\csc x - \cot x| + C \) dan untuk integral \( \int \csc x \cot^2 x \ dx \) dapat kita selesaikan menggunakan teknik integral parsial dengan memisalkan \( u = \cot x \) dan \( dv = \csc x \cot x \ dx \) sehingga kita peroleh:

Dengan demikian, integral dari \( \csc^3 x \), yakni:
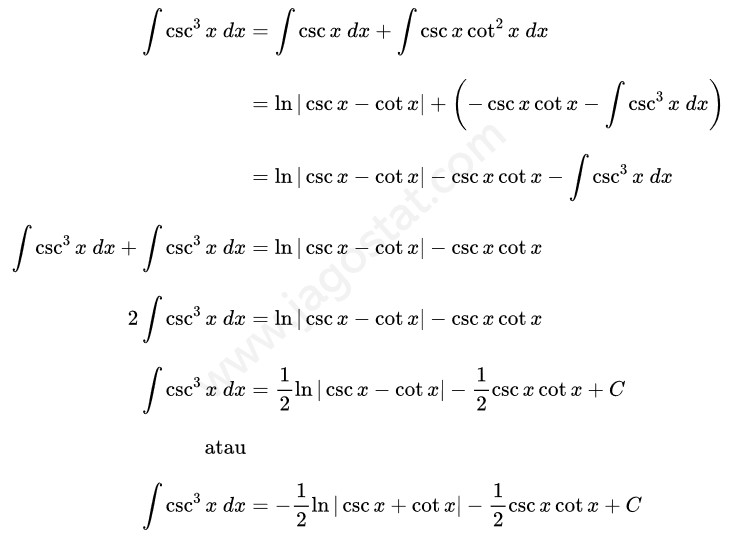
Contoh 16:
Tentukan \( \int \csc^4 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \csc^4 x \) menjadi \( \csc^2 x \cdot \csc^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti fungsi \( \csc^2 x \) menjadi \( (\cot^2 x + 1) \). Kita peroleh hasil berikut:

Dari hasil di atas, sekarang kita akan mencari \( \int \csc^2 x \ dx \) dan \( \int \cot^2 x \csc^2 x \ dx \). Dari Contoh 14 di atas \( \int \csc^2 x \ dx = -\cot x + C \) dan untuk integral \( \int \cot^2 x \csc^2 x \ dx \) dapat kita selesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \cot x \) sehingga kita peroleh:
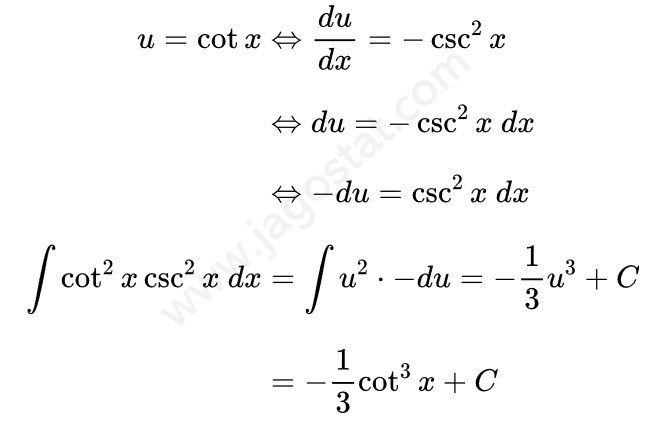
Dengan demikian, integral dari \( \csc^4 x \), yakni:

Contoh 17:
Tentukan \( \int \csc^5 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \csc^5 x \) menjadi \( \csc^3 x \cdot \csc^2 x \) terlebih dahulu. Kemudian selesaikan integral tersebut menggunakan teknik integral parsial dengan memisalkan \( u = \csc^3 x \) dan \( dv = \csc^2 x \ dx \). Kita peroleh hasil berikut:

Dari hasil di atas, kita peroleh berikut ini:

Dari Contoh 15 di atas, kita telah memperoleh hasil \( \int \csc^3 x \ dx \) sehingga integral dari \( \csc^5 x \), yakni:
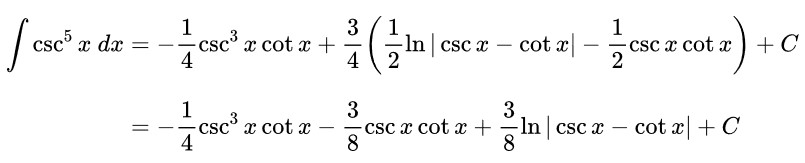
Atau karena \( \int \csc^3 x \ dx \) juga sama dengan

maka, hasil yang kita peroleh sebelumnya juga dapat dituliskan menjadi:
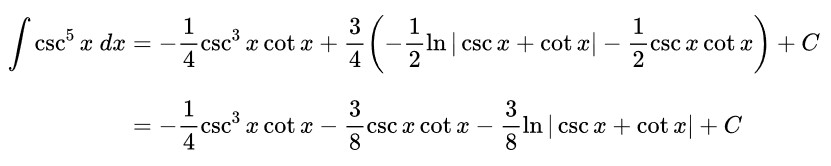
Baca juga:
Contoh 18:
Tentukan \( \int \csc^6 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \csc^6 x \) menjadi \( (\csc^2 x)^2 \cdot \csc^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti fungsi \( \csc^2 x \) menjadi \( (1+\cot^2 x) \). Kita peroleh hasil berikut:
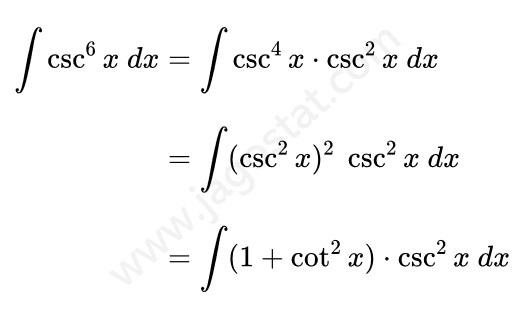
Untuk menyelesaikan integral \( \int (1+\cot^2 x) \cdot \csc^2 x \ dx \), kita dapat menggunakan teknik integral substitusi dengan memisalkan \( u = \cot x \) sehingga kita peroleh:

Contoh 19:
Tentukan \( \int \sec^2 x \ dx \).
Pembahasan:
\begin{aligned} \int \sec^2 x \ dx = \tan x + C \end{aligned}
Contoh 20:
Tentukan \( \int \sec^3 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \sec^3 x \) menjadi \( \sec x \cdot \sec^2 x \) terlebih dahulu. Kemudian selesaikan integral tersebut menggunakan teknik integral parsial dengan memisalkan \( u = \sec x \) dan \( dv = \sec^2 x \ dx \). Kita peroleh hasil berikut:
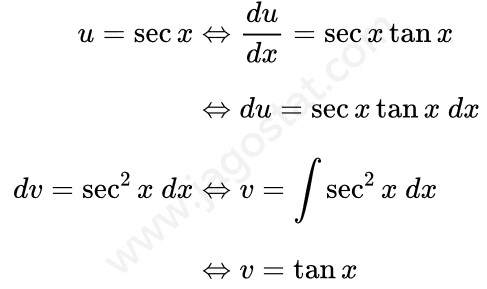
Dari hasil di atas, penyelesaian dari \( \int \sec^3 x \ dx \), yaitu:
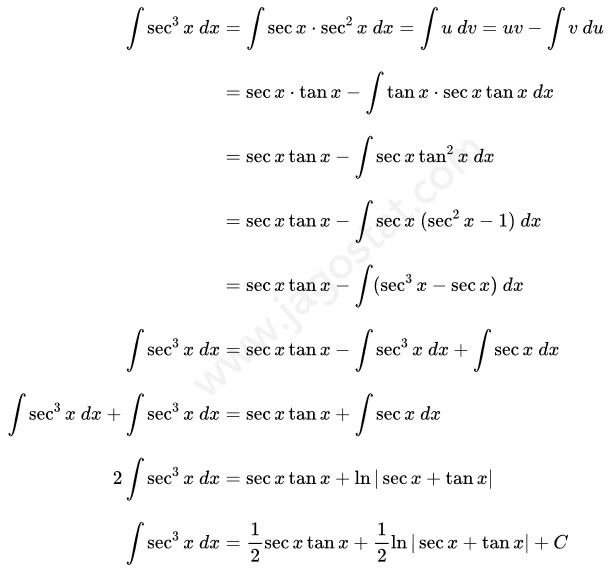
Catatan: Hasil dari \( \int \sec x \ dx = \ln |\sec x + \tan x| + C \).
Contoh 21:
Tentukan \( \int \sec^4 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \sec^4 x \) menjadi \( \sec^2 x \cdot \sec^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti fungsi \( \sec^2 x \) menjadi \( (\tan^2 x + 1) \). Kita peroleh hasil berikut:
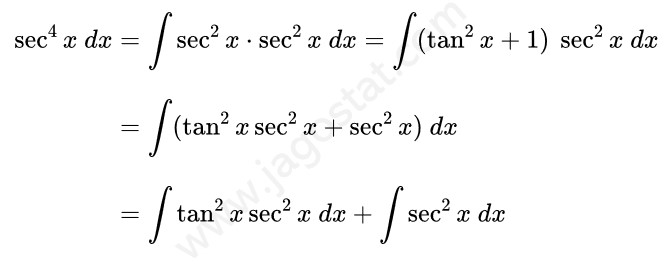
Dari hasil di atas, sekarang kita akan mencari \( \int \tan^2 x \sec^2 x \ dx \) dan \( \int \sec^2 x \ dx \). Dari Contoh 19, di atas \( \int \sec^2 x \ dx = \tan x + C \) dan untuk integral \( \int \tan^2 x \sec^2 x \ dx \) dapat kita selesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \tan x \) sehingga diperoleh:
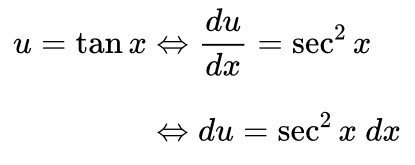
Dengan demikian, integral dari \( \sec^4 x \), yakni:

Contoh 22:
Tentukan \( \int \sec^5 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \sec^5 x \) menjadi \( \sec^3 x \cdot \sec^2 x \) terlebih dahulu. Kemudian selesaikan integral tersebut menggunakan teknik integral parsial dengan memisalkan \( u = \sec^3 x \) dan \( dv = \sec^2 x \ dx \). Kita peroleh hasil berikut:
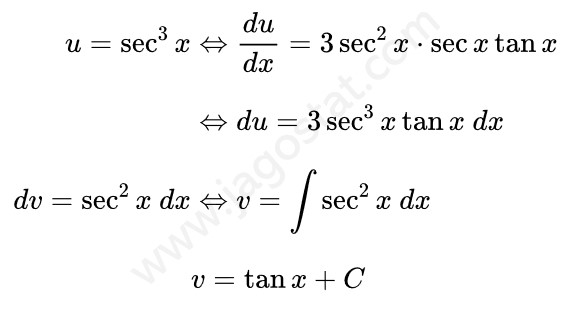
Dari hasil di atas, kita peroleh berikut ini:

Dari Contoh 20 di atas, kita telah memperoleh hasil \( \int \sec^3 x \ dx \) sehingga integral dari \( \sec^5 x \), yakni:

Contoh 23:
Tentukan \( \int \sec^6 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita uraikan fungsi \( \sec^6 x \) menjadi \( (\sec^2 x)^2 \cdot \sec^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti fungsi \( \sec^2 x \) menjadi \( (\tan^2 x + 1) \). Kita peroleh hasil berikut:

Untuk menyelesaikan integral \( \int (\tan^2 x + 1) \cdot \sec^2 x \ dx \), kita dapat menggunakan teknik integral substitusi dengan memisalkan \( u = \tan x \) sehingga kita peroleh:
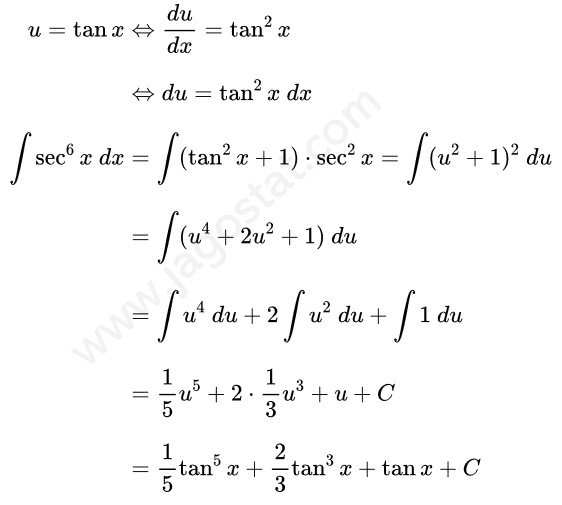
Baca juga:
Contoh 24:
Tentukan \( \int \cot^2 x \ dx \).
Pembahasan:
Dari rumus identitas trigonometri, kita tahu bahwa \( \cot^2 = \csc^2 x - 1 \) sehingga kita peroleh berikut ini:

Contoh 25:
Tentukan \( \int \cot^3 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita jabarkan fungsi \( \cot^3 x \) menjadi \( \cot x \cdot \cot^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti \( \cot^2 x \) menjadi \( (\csc^2 x - 1) \). Kita peroleh hasil berikut:

Integral dari \( \cot x \) sama dengan \( \ln |\sin x| + C \) dan untuk \(\int \cot x \csc^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \cot x \) sehingga kita peroleh:
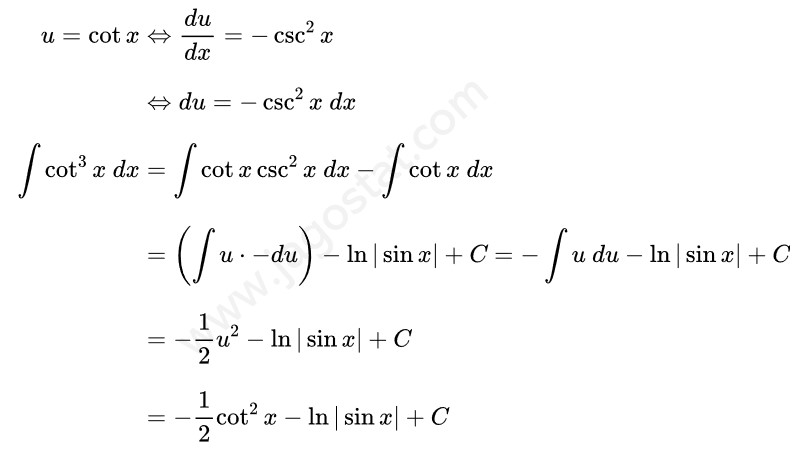
Contoh 26:
Tentukan \( \int \cot^4 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita jabarkan fungsi \( \cot^4 x \) menjadi \( \cot^2 x \cdot \cot^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti \( \cot^2 x \) menjadi \( (\csc^2 x - 1) \). Kita peroleh hasil berikut:
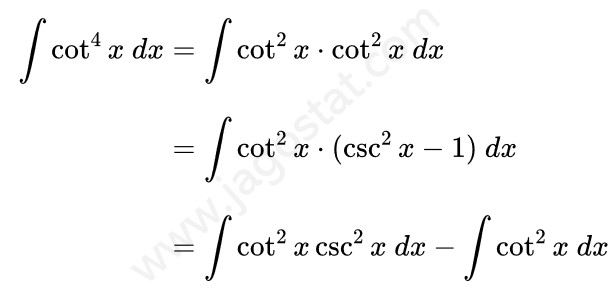
Dari hasil di atas, ada dua integral yang akan kita selesaikan. Dalam Contoh 24, \( \int \cot^2 x \ dx = -\cot x - x + C \) dan untuk \( \int \cot^2 x \csc^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \cot x \) sehingga diperoleh:

Contoh 27:
Tentukan \( \int \cot^5 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita jabarkan fungsi \( \cot^5 x \) menjadi \( \cot^3 x \cdot \cot^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti \( \cot^2 x \) menjadi \( (\csc^2 x - 1) \). Kita peroleh hasil berikut:

Dari hasil di atas, ada dua integral yang akan kita selesaikan. Dalam Contoh 25, \( \int \cot^3 x \ dx = -\frac{1}{2} \cot^2 x - \ln|\sin x| + C \) dan untuk \( \int \cot^3 x \csc^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \cot x \) sehingga diperoleh:

Contoh 28:
Tentukan \( \int \cot^6 x \ dx \).
Pembahasan:
Untuk menyelesaikan integral ini kita jabarkan fungsi \( \cot^6 x \) menjadi \( \cot^4 x \cdot \cot^2 x \) terlebih dahulu. Lalu berdasarkan rumus identitas trigonometri, ganti \( \cot^2 x \) menjadi \( (\csc^2 x - 1) \). Kita peroleh hasil berikut:

Dari hasil di atas, ada dua integral yang akan kita selesaikan. Dalam Contoh 26, \( \int \cot^4 x \ dx = -\frac{1}{3} \cot^3 x + \cot x + x + C \) dan untuk \( \int \cot^4 x \csc^2 x \ dx \) dapat diselesaikan menggunakan teknik integral substitusi dengan memisalkan \( u = \cot x \) sehingga diperoleh:
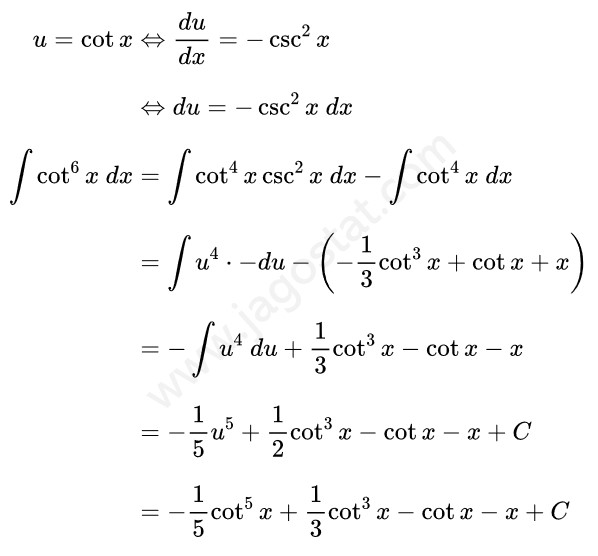
Jika Anda merasa artikel ini bermanfaat, bantu klik tombol suka di bawah ini dan jika ada yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.
Artikel terkait
Inside of every problem lies an opportunity.
