Kalkulus I   »   Teknik Pengintegralan   ›  Pembuktian Rumus Reduksi Integral Trigonometri

Pembuktian Rumus Reduksi Integral Trigonometri

Rumus reduksi kerap kali dijumpai ketika menggunakan pengintegralan parsial. Berikut ini kita membahas rumus reduksi beserta pembuktiannya dengan pengintegralan parsial.

Rumus reduksi kerap kali dijumpai ketika menggunakan pengintegralan parsial. Berikut ini kita membahas rumus reduksi beserta pembuktiannya dengan pengintegralan parsial.

Pembuktian Rumus 1

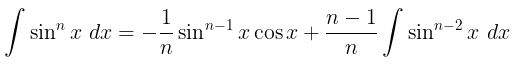
Perhatikan bahwa kita bisa menuliskan

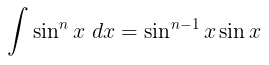
Selanjutnya, gunakan integral parsial. Misalkan: \(u=\sin^{n-1} ⁡x\) dan \(v = \int \sin{⁡x} \ dx\), maka

Dengan demikian, kita peroleh

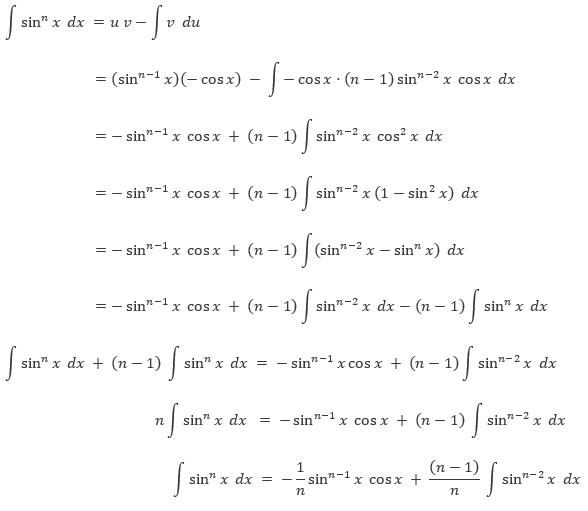
Pembuktian Rumus 2

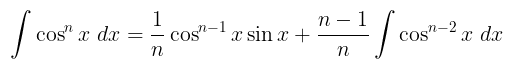
Perhatikan bahwa kita bisa menuliskan

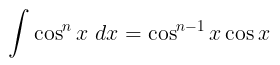
Selanjutnya, gunakan integral parsial. Misalkan: \(u=\cos^{n-1} ⁡x\) dan \(v = \int \cos{⁡x} \ dx\), maka

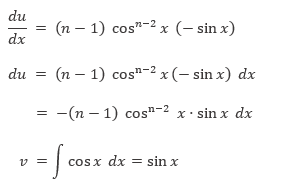
Dengan demikian, kita peroleh

Pembuktian Rumus 3

Perhatikan bahwa

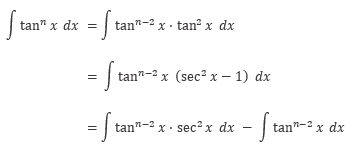
Misalkan: \(u=\tan{⁡x}\), maka

Dengan demikian, kita peroleh

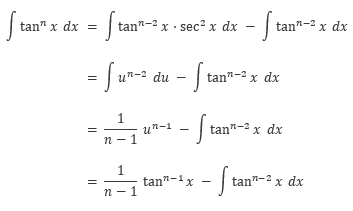
Pembuktian Rumus 4

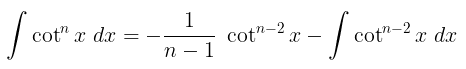
Perhatikan bahwa

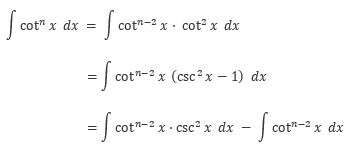
Misalkan: \(u=\cot{⁡x}\), maka

Dengan demikian, kita peroleh

Pembuktian Rumus 5

Perhatikan bahwa

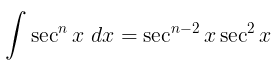
Gunakan integral parsial. Misalkan: \(u=\sec^{n-2} ⁡x\) dan \(v = \int \sec^2{⁡x} \ dx\), maka

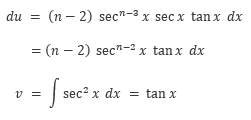
Dengan demikian, kita peroleh

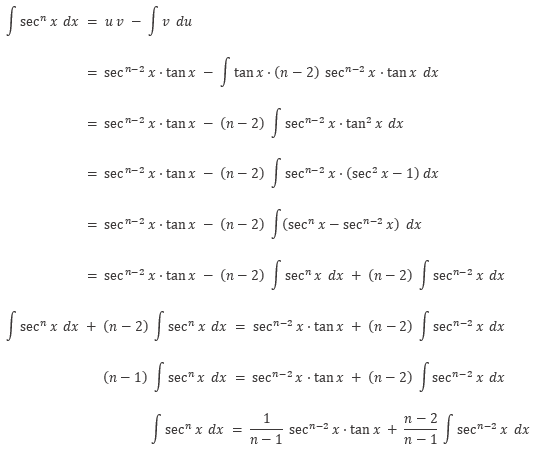
Pembuktian Rumus 6

Perhatikan bahwa

Gunakan integral parsial. Misalkan: \(u=\csc^{n-2} ⁡x\) dan \(v = \int \csc^2{⁡x} \ dx\), maka

Dengan demikian, kita peroleh

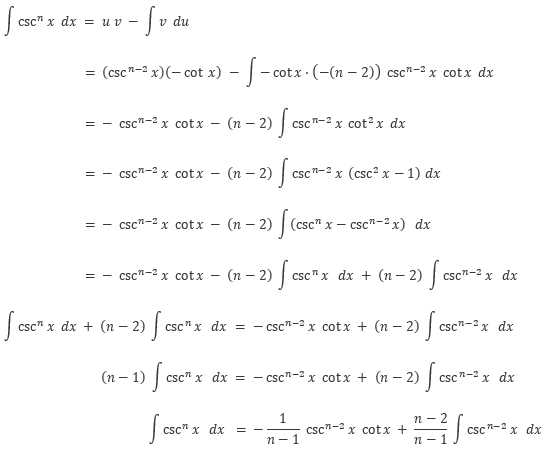
Sumber:

Purcell, Edwin J., Dale Verberg., dan Steve Rigdon. (2007). Calculus, ed 9. Penerbit Pearson.

Jika Anda merasa artikel ini bermanfaat, klik tombol suka di bawah ini dan jika ada pembahasan yang kurang jelas dari artikel ini silahkan tanyakan di kolom komentar. Terima kasih.