Contoh 1:

Anggap $X_i \sim BIN (1,p)$. Tentukan estimator maksimum likelihoodnya (MLE).

Pembahasan:

Karena peubah acak $X_i$ berdistribusi binomial dengan n = 1 atau disebut juga berdistribusi Bernoulli, maka fungsi kepadatan peluangnya yaitu

Untuk mencari estimator maksimum likelihood, kita ikuti beberapa langkah yang telah dijelaskan di atas, yakni

Langkah 1: Tentukan fungsi likelihood

Langkah 2: Tentukan $\ln L(p)$

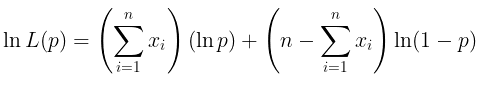
Langkah 3: Maksimumkan fungsi $\ln L(p)$

Untuk memaksimumkan fungsi $\ln L(p)$, kita mencari turunan pertamanya kemudian menyamakannya dengan nol. Setelah itu, kita selesaikan persamaan untuk mendapatkan estimator yang diinginkan.

Langkah 4: Tentukan $\hat{p}$

Jadi, estimator maksimum likelihood nya yaitu $\hat{p}_{MLE} = \overline{x}$.

Contoh 2:

Anggap $X_1, …, X_n$ adalah sampel acak dari distribusi eksponensial.

Tentukan $\hat{θ}_{MLE}$.

Pembahasan:

Langkah 1: Tentukan fungsi likelihood

Langkah 2: Tentukan $\ln L(θ)$

Langkah 3: Maksimumkan fungsi $\ln L(θ)$

Untuk memaksimumkan fungsi $\ln L(θ)$, kita mencari turunan pertamanya kemudian menyamakannya dengan nol. Setelah itu, kita selesaikan persamaan untuk mendapatkan estimator yang diinginkan.

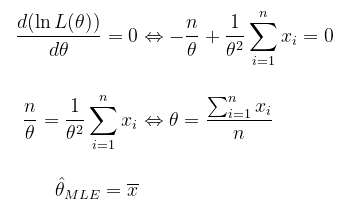
Langkah 4: Tentukan $\hat{θ}$

Jadi, estimator maksimum likelihood nya yaitu $\hat{\theta}_{MLE} = \overline{x}$.

Contoh 3:

Anggap $X_1, …, X_n$ adalah random sampel dari distribusi normal dengan parameter $(θ_1, θ_2)$, yakni $X_i \sim N(θ_1, θ_2)$. Tentukan $\hat{θ}_1$ dan $\hat{θ}_2$ dengan menggunakan metode maksimum likehood.

Pembahasan:

Fungsi kepadatan peluang dari distribusi normal dengan parameter $(θ_1, θ_2)$, yaitu

Langkah 1: Tentukan fungsi likelihood

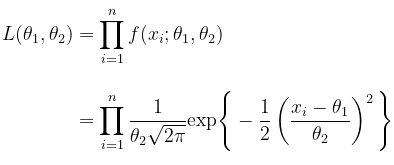
Langkah 2: Tentukan $\ln L(\theta_1,\theta_2)$

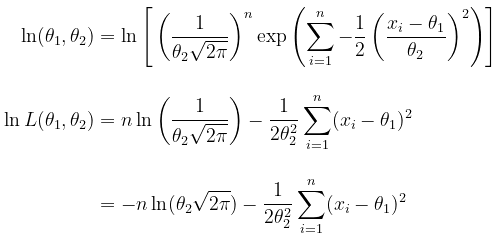
Langkah 3: Maksimumkan fungsi $\ln L(\theta_1,\theta_2)$

Untuk memaksimumkan fungsi $\ln L(\theta_1,\theta_2)$, kita mencari turunan pertama masing-masing terhadap $\theta_1$ dan $\theta_2$, kemudian menyamakannya dengan nol. Setelah itu, kita selesaikan persamaan untuk mendapatkan estimator yang diinginkan.

Dari hasil penghitungan diperoleh turunan pertama terhadap $\theta_1$ dan terhadap $\theta_2$, yaitu:

Dengan membuat kedua turunan ini sama dengan nol dan menyelesaikan ini secara simultan; akan diperoleh MLE bagi $θ_1$ dan $θ_2$ sebagai berikut:

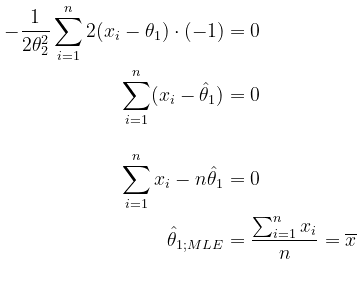
Jadi, penduga maksimum likelihood bagi parameter $\hat{θ}_1$ adalah $\overline{x}$.

Jadi, penduga maksimum likelihood bagi parameter $\hat{θ}_2$ adalah $\sqrt{\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n}}$.