Statistika Matematika II   »   Kriteria Estimator yang Ideal   ›  Keluarga Eksponensial

Exponential Family

Keluarga Eksponensial

Beberapa fungsi distribusi yang termasuk keluarga eksponensial di antaranya yaitu distribusi Bernoulli, Binomial, Binomial Negatif, Poisson, Normal, Eksponensial, Gamma dan Uniform.

Suatu distribusi disebut sebagai anggota keluarga eksponensial (exponential family) \(k\) parameter bila fungsi kepadatan peluangnya (probability density function, pdf) dapat dinyatakan dalam bentuk sebagai berikut.

dimana:

\(a(θ)\) : fungsi non negatif dari \(θ\)

\(b(x)\) : fungsi non negatif dari \(x\)

\(c_i(θ)\): fungsi riil dari \(θ\)

\(d_i(x)\): fungsi riil dari \(x\)

Beberapa fungsi distribusi yang termasuk keluarga eksponensial di antaranya yaitu distribusi Bernoulli, Binomial, Binomial Negatif, Poisson, Normal, Eksponensial, Gamma dan Uniform. Berikut ini kita akan membuktikan beberapa contoh distribusi yang termasuk keluarga eksponensial.

Contoh 1:

Selidikilah apakah \(X_1, …, X_n \sim POI(λ)\) merupakan keluarga eksponensial satu parameter.

Pembahasan:

Pdf dari \(X_1, …, X_n \sim POI(λ)\) yaitu:

yang mana bisa dinyatakan dalam bentuk

Karena pdf dari \(X_1, …, X_n \sim POI(λ)\) dapat dinyatakan dalam bentuk

di mana:

Dengan demikian, \(X_1, …, X_n \sim POI(λ)\) merupakan bagian dari keluarga eksponensial satu parameter.

Contoh 2:

Selidikilah apakah \(X_i \sim BIN(1,p) \) merupakan keluarga eksponensial.

Pembahasan:

Pdf dari \(X_i \sim BIN(1,p) \) yaitu:

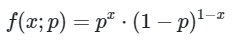
yang mana bisa dinyatakan dalam bentuk

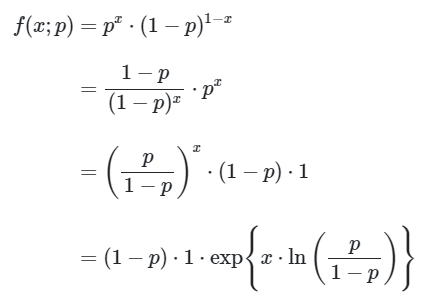
Karena pdf dari \(X_i \sim BIN(1,p) \) dapat dinyatakan dalam bentuk

di mana:

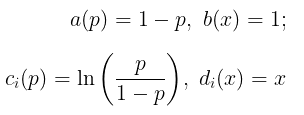
Dengan demikian, \(X_i \sim BIN(1,p) \) merupakan bagian dari keluarga eksponensial satu parameter.

Contoh 3:

Periksalah apakah \(X_i \sim N(μ, σ^2)\) merupakan keluarga eksponensial dua parameter.

Pembahasan:

Pdf dari \(X_i \sim N(μ, σ^2)\) yaitu:

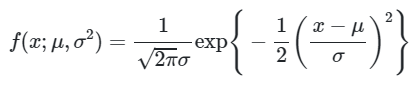
yang mana bisa dinyatakan dalam bentuk

Karena pdf dari \(X_i \sim N(μ, σ^2)\) dapat dinyatakan dalam bentuk

di mana:

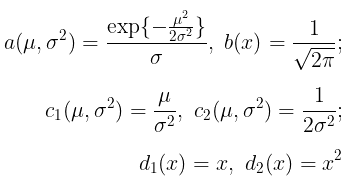
Dengan demikian, \(X_i \sim N(μ, σ^2)\) merupakan bagian dari keluarga eksponensial dua parameter.

Contoh 4:

Periksalah apakah \(X_i \sim Gamma(α, β)\) merupakan keluarga eksponensial dua parameter.

Pembahasan:

Pdf dari \(X_i \sim Gamma(α, β)\) yaitu:

yang mana bisa dinyatakan dalam bentuk

Karena pdf dari \(X_i \sim Gamma(α, β)\) dapat dinyatakan dalam bentuk

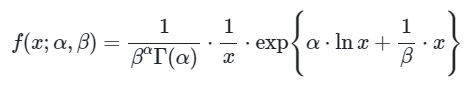
di mana:

Dengan demikian, \(X_i \sim Gamma(α, β)\) merupakan bagian dari keluarga eksponensial dua parameter.

Cukup sekian ulasan singkat mengenai keluarga eksponensial (exponential family) dalam artikel ini. Terima kasih telah membaca sampai selesai. Jika Anda merasa artikel ini bermanfaat, boleh dibantu share ke teman-temannya, supaya mereka juga bisa belajar dari artikel ini.