
www.jagostat.com
www.jagostat.com
Website Belajar Matematika & Statistika
Website Belajar Matematika & Statistika
Cari artikel...
STATISTIKA MATEMATIKA II
Statistika Matematika II
Pendugaan Titik
Kriteria Pendugaan yang Ideal
Pendugaan Interval
Statistika Matematika II » Estimasi Titik › Metode Momen (Method of Moment Estimation)
Joki Tugas Matematika Murah, Hanya Rp10-50 Ribu. Hub. WA: 0812-5632-4552
Point Estimate
Metode Momen (Method of Moment Estimation)
Dalam statistika, terdapat beberapa metode untuk mengestimasi parameter populasi. Salah satu dari metode tersebut dikenal dengan metode momen (method of moments estimation, MME).
Dalam statistika, terdapat beberapa metode untuk mengestimasi parameter populasi. Salah satu dari metode tersebut dikenal dengan metode momen (method of moments estimation, MME). Metode ini merupakan sebuah prosedur yang sangat sederhana untuk mencari estimator atau penduga bagi satu atau lebih parameter populasi.
Metode momen ini didasarkan pada gagasan bahwa momen sampel \((M'_r)\) seharusnya memberikan perkiraan yang baik terhadap momen populasi \((\mu'_r)\) yang bersesuaian, yakni \(M'_r\) seharusnya merupakan estimator yang baik bagi \(\mu'_r\) untuk \( r = 1,2,... \).
Dengan demikian, metode ini dimulai dengan menyatakan momen populasi dan momen sampel terlebih dahulu. Kemudian menyamakan momen populasi dengan momen sampel sehingga diperoleh persamaan \(\mu'_r = M'_r\). Dengan menyelesaikan persamaan tersebut akan diperoleh estimator yang akan dicari. Jadi, tahapan untuk menerapkan metode momen ini, yaitu:
- Tentukan momen populasi
- Tentukan momen sampel
- Menyamakan momen populasi dan momen sampel, kemudian menyelesaikan persamaan untuk mencari estimator yang diinginkan
Kita definisikan momen populasi dan momen sampel sebagai berikut:
Definisi: Momen Populasi
Momen populasi ke-\(r\) terhadap asal (raw moments atau moments about the origin) dari suatu peubah acak (random variable) \(X\), yaitu
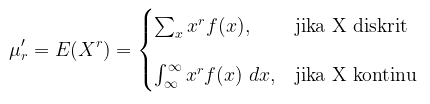
dan momen populasi ke-\(r\) terhadap rata-rata (central moments atau the moments about its mean), yaitu:

Definisi: Momen Sampel
Jika \(X_1, …,X_n\) adalah sampel acak (random samples) dari \(f(x; θ_1,…,θ_k)\), maka momen sampel ke-\(r\) diberikan oleh

Contoh Soal dan Pembahasan
Berikut ini diberikan beberapa contoh kasus terkait metode momen. Pertama kita akan melihat kasus untuk satu parameter pada Contoh 1 sampai 3. Setelah itu, kita lanjutkan ke kasus untuk dua parameter pada Contoh 4.
Contoh 1:
Misalkan \(X_1, …,X_n\) adalah sampel acak (random samples) dari populasi yang berdistribusi tertentu dengan fungsi kepadatan peluangnya (probability density function, pdf) sebagai berikut:
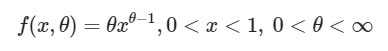
Dengan menggunakan metode momen, tentukan estimator titik bagi parameter \(θ\).
Pembahasan:
Langkah 1: Tentukan momen populasi
Karena di sini hanya terdapat satu parameter populasi \((θ)\), maka kita hanya perlu mencari momen populasi pertama yang mana sama dengan nilai harapan dari \(X\), yakni
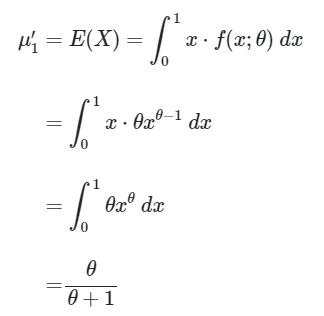
Langkah 2: Tentukan momen sampel
Seperti sudah dijelaskan dalam definisi di atas, maka momen sampelnya yaitu:

Langkah 3: Menyamakan momen populasi dengan momen sampel
Dengan menyamakan momen populasi dan momen sampel, maka akan diperoleh estimator yang diinginkan.

Jadi, estimator titik bagi parameter \(θ\) adalah \(\hat{θ}_{MME} = \frac{\overline{x}}{1-\overline{x}}\).
Contoh 2:
Misalkan \(X_1, …, X_n\) adalah sampel acak (random samples) dari populasi yang berdistribusi eksponensial dengan parameter \(θ\), yakni \(X_i \sim EXP(θ) \). Dengan menggunakan metode momen, tentukan estimator titik bagi parameter \(θ\).
Pembahasan:
Langkah 1: Tentukan momen populasi
Karena di sini hanya terdapat satu parameter populasi \((θ)\), maka kita hanya perlu mencari momen populasi pertama yang mana sama dengan nilai harapan dari \(X\), yakni
\[ μ_1' = E(X) = θ \]
Langkah 2: Tentukan momen sampel
Seperti sudah dijelaskan dalam definisi di atas, maka momen sampelnya yaitu:

Langkah 3: Menyamakan momen populasi dengan momen sampel
Dengan menyamakan momen populasi dan momen sampel, maka akan diperoleh estimator yang diinginkan.

Jadi, estimator titik bagi parameter \(θ\) adalah \(\hat{θ}_{MME} = \overline{x}\).
Contoh 3:
Misalkan \(X_1, …, X_n\) adalah sampel acak dari populasi yang berdistribusi Poisson dengan parameter \(θ\). Dengan menggunakan metode momen, tentukan estimator titik bagi parameter \(θ\).
Pembahasan:
Fungsi kepadatan peluang (pdf) distribusi Poisson yaitu

Langkah 1: Tentukan momen populasi
Karena di sini hanya terdapat satu parameter populasi \((θ)\), maka kita hanya perlu mencari momen populasi pertama yang mana sama dengan nilai harapan dari \(X\), yakni

Langkah 2: Tentukan momen sampel
Seperti sudah dijelaskan dalam definisi di atas, maka momen sampelnya yaitu:

Langkah 3: Menyamakan momen populasi dengan momen sampel
Dengan menyamakan momen populasi dan momen sampel, maka akan diperoleh estimator yang diinginkan.

Jadi, estimator titik bagi parameter \(θ\) adalah \(\hat{θ}_{MME} = \overline{x}\).
Contoh 4:
Misalkan \(X_1, …, X_n\) adalah sampel acak dari populasi yang berdistribusi normal dengan rata-rata \(μ\) dan varians \(σ^2\). Dengan menggunakan metode momen, tentukan estimator titik bagi parameter \(μ\) dan \(σ^2\).
Pembahasan:
Pdf distribusi normal \(X_i \sim N(μ,σ^2)\) yaitu:

Langkah 1: Tentukan momen populasi
Karena di sini terdapat dua parameter populasi yakni \(μ\) dan \(σ^2\), maka kita perlu mencari momen populasi pertama dan kedua, yakni
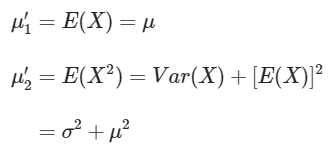
Langkah 2: Tentukan momen sampel
Karena terdapat dua parameter, maka kita perlu mencari momen sampel pertama dan kedua, yakni
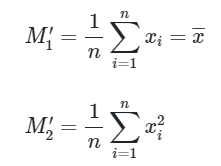
Langkah 3: Menyamakan momen populasi dengan momen sampel
Dengan menyamakan momen populasi dan momen sampel, maka akan diperoleh estimator yang diinginkan.
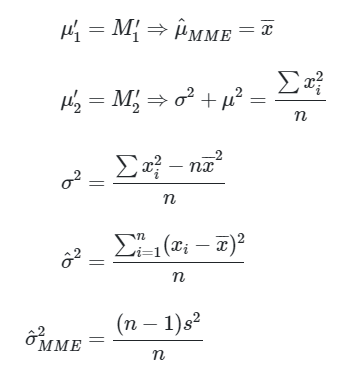
Jadi, estimator titik bagi parameter \(μ\) adalah \(\hat{μ}_{MME} = \overline{x}\) dan estimator titik bagi parameter \(σ^2\) yaitu \(\hat{σ}^2_{MME} = \frac{(n-1) s^2}{n}\).
Cukup sekian penjelasan mengenai metode momen untuk mencari estimator bagi suatu parameter populasi dalam artikel ini. Terima kasih telah membaca sampai selesai. Jika Anda merasa artikel ini bermanfaat, boleh dibantu share ke teman-temannya, supaya mereka juga bisa belajar dari artikel ini.
Artikel Terkait
No one has the power to shatter your dreams unless you give it to them.
Maeve Greyson